
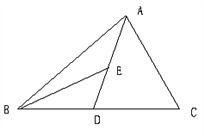
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
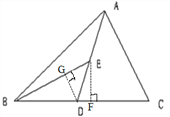
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?
【答案】(1)∠BED=55°;(2)画图见解析;(3)EF=4,DG=![]() .
.
【解析】试题分析:(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线,过D作BE边的垂线即可;
(3)根据三角形中线性质求出△BDE的面积,再由三角形的面积公式求出高即可.
试题解析:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)画图如下:
(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴△ABD的面积=![]() △ABC的面积=20,△BDE的面积=
△ABC的面积=20,△BDE的面积=![]() △ABD的面积=10,
△ABD的面积=10,
∴![]() BD·EF=10,
BD·EF=10, ![]() ×5EF=10,
×5EF=10,
解得EF=4,
![]() BE·DG=10,
BE·DG=10, ![]() ×6 DG =10,
×6 DG =10,
EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示-5,点B表示10.动点P从点A出发,沿数轴正方向以每秒1个单位的速度匀速运动;同时,动点Q从点B出发,沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.
(1)当t为 秒时,P,Q两点相遇,求出相遇点所对应的数;
(2)当t为何值时,P,Q两点的距离为3个单位长度,并求出此时点P对应的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,O为原点,现A,B两点分别以1个单位长度/秒的速度同时向左运动。
(1)几秒后,原点恰好在A,B两点正中间?
(2)几秒后,恰好有OA:OB=1:2.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O与直线l相切于A点,点P、Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动.连接OQ、OP(如图),则阴影部分面积S1、S2的大小关系是( )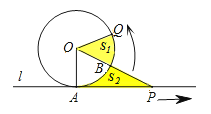
A.S1=S2
B.S1≤S2
C.S1≥S2
D.先S1<S2 , 再S1=S2 , 最后S1>S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)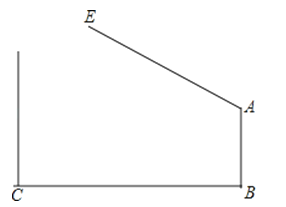
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2015的值为( )
A. ﹣2015 B. ﹣2014 C. ﹣1007 D. ﹣1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: ①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )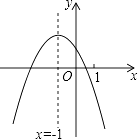
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com