
【题目】如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.若连接AM,则AM是否平分∠DAB?并说明理由.
【答案】解:AM平分∠DAB.理由如下:
过点M作ME⊥AD,垂足为E. 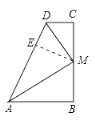
∵∠CDM=∠EDM,MC⊥CD,ME⊥AD,
∴ME=MC.
∵M是BC的中点,
∴MC=MB.
∴ME=MB.
又∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB.
【解析】AM平分∠DAB.理由如下:过点M作ME⊥AD,垂足为E. 根据角平分线上的点到角两边的距离相等得出 ME=MC.根据中点的定义得出 MC=MB.从而得出 ME=MB.然后根据到角两边距离相等的点在这个角的角平分线上得出 AM平分∠DAB.
【考点精析】本题主要考查了角的平分线判定和角平分线的性质定理的相关知识点,需要掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,李明计划在张村E、李村F之间建一家超市,张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置(简要说明作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为_____.
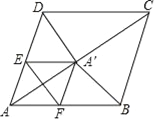
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民区道路上的“早市”引起了大家关注,小明想了解本小区居民对“早市”的看法,进行了一次抽样调查,把居民对“早市”的看法分为四个层次:A、非常赞同B、赞同但要有一定的限制;C、无所谓D、不赞同,并将调查结果绘制了图1和图2两幅不完整的统计图.
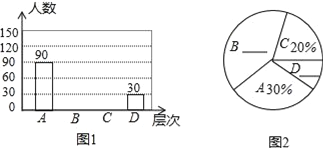
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“早市”的看法表示赞同(包括A层次).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE⊥AC垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF 正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com