
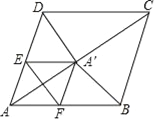
【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为_____.
【答案】![]() 或
或![]() .
.
【解析】首先证明四边形AEA′F是菱形,分两种情形:①CA′=CD,②A′C=A′D分别计算即可.
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CD=CA′时,∵AA′=AC﹣CA′=3,
∴AP=![]() AA′=
AA′=![]() .
.
②当A′C=A′D时,∵∠A′CD=∠A′DC=∠DAC,
∴△A′CD∽△DAC,
∴![]() =
=![]() ,
,
∴A′C=![]() ,
,
∴AA=8﹣![]() =
=![]() ,
,
∴AP=![]() AA′=
AA′=![]() .
.
故答案为![]() 或
或![]() .
.
“点睛”本题考查菱形的性质、翻折变换、等腰三角形的判断和性质等知识,解题的关键是学会分类讨论,不能漏解. 属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.
(1)直接写出抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,点E的速度为每秒![]() 个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com