
【题目】如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= . 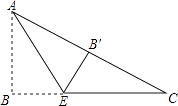
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①等腰三角形的腰长大于底边长;
②三条线段![]() 、
、![]() 、
、![]() ,如果
,如果![]() ,那么这三条线段一定可以组成三角形;
,那么这三条线段一定可以组成三角形;
③等腰三角形是轴对称图形,它的对称轴是底边上的高;
④面积相等的两个三角形全等.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
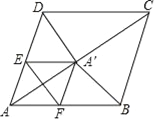
【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民区道路上的“早市”引起了大家关注,小明想了解本小区居民对“早市”的看法,进行了一次抽样调查,把居民对“早市”的看法分为四个层次:A、非常赞同B、赞同但要有一定的限制;C、无所谓D、不赞同,并将调查结果绘制了图1和图2两幅不完整的统计图.
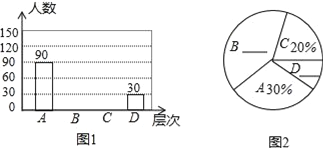
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“早市”的看法表示赞同(包括A层次).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.
斐波那契数列中的第n个数可以用 ![]() [
[ ![]() ﹣
﹣ ![]() ]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为80 m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示:
(1)从上述统计图中可知:每人每分能擦课桌椅m2;擦玻璃、擦课桌椅、扫地拖地的面积分别是m2、m2、m2;
(2)如果x人每分钟擦玻璃的面积是y m2 , 那么y关于x的函数关系式是;
(3)他们一起完成扫地和拖地的任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅.如果你是卫生委员,该如何分配这两组的人数才能最快地完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com