
【题目】如图,PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.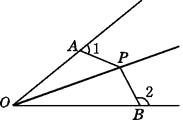
【答案】证明:过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,则∠AEP=∠BFP=90°. 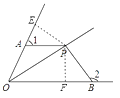
∵∠1+∠2=180°,∠2+∠PBO=180°,
∴∠1=∠PBO.
在△PAE和△PBF中, 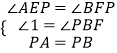
∴△PAE≌△PBF(AAS).
∴PE=PF.
∴OP为∠AOB的平分线,即OP平分∠AOB.
【解析】过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,则∠AEP=∠BFP=90°. 根据邻补角的定义得出∠2+∠PBO=180°,又因∠1+∠2=180°,根据同角的补角相等得出∠1=∠PBO.然后根据AAS判断出△PAE≌△PBF,根据全等三角形对应角相等得出PE=PF.根据到角两边距离相等的点在这个角的角平分线上得出OP为∠AOB的平分线,即OP平分∠AOB.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是_________毫米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列能断定△ABC为等腰三角形的是( )
A. ∠A=30、∠B=60 B. ∠A=50、∠B=80
C. AB=AC=2,BC=4 D. AB=3、BC=7,周长为13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com