
【题目】请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中, AD是角平分线.
求证: ![]() .
.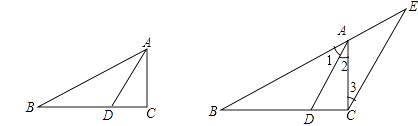
证明:过C作CE∥DA,交BA的延长线于E.
∴ ![]() . ①
. ①![]() AD是角平分线,
AD是角平分线,
∴ ![]() .
.![]()
![]() .
.![]() . ②
. ②
又 ![]() ,
,![]() . ③
. ③![]()
![]() .
.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABD和△ACD面积的比来证明三角形内角平分线定理.
【答案】
(1)解:证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
③平行线分线段成比例定理
(2)解:∵AD是角平分线,
∴ ![]() ,
,
又∵AB=7cm,AC=4cm,BC=6cm,
∴ ![]() ,
,
∴BD= ![]() (cm)
(cm)
(3)解:∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= 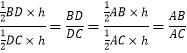 ,
,
可得: ![]()
【解析】(1)利用“平行线的性质定理;等腰三角形的判定定理;平行线分线段成比例定理”可填出答案;(2)学会应用(1)的结论,构造比例式求线段;(3)利用面积法,再结合角平分线性质定理可构造两个比例式,证得结论.
【考点精析】利用三角形的面积和角平分线的性质定理对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
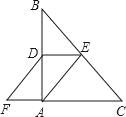
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?( ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, 在 ![]() 中,
中, ![]() ,
, ![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ![]() ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头” .两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)直接写出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请你画出树状图求出一次游戏中甲、乙、丙三人出第一次手势时, 不分胜负的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ![]()
![]() ,④
,④ ![]()
![]() , ⑤
, ⑤ ![]()
![]() ,使△ADE与△ACB一定相似的有( )
,使△ADE与△ACB一定相似的有( )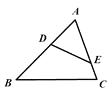
A.①②④
B.②④⑤
C.①②③④
D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°.将△ABC绕点C逆时针旋转得到△A’B’C,旋转角为 ![]() ,且0°<
,且0°< ![]() <180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
<180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
(1)求∠A的度数;
(2)当点C到AA’的距离等于AC的一半时,求 ![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com