
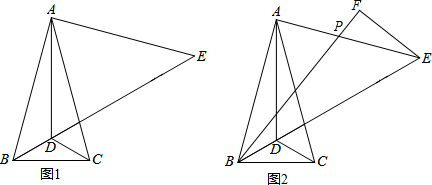
分析 (1)易求∠ABD的大小,易求AD所在直线垂直平分BC,根据等腰三角形底边三线合一性质可得AD平分∠BAC,根据三角形外角等于不相邻两内角性质即可解题;
(2)在线段DE上截取DM=AD,连接AM,易证△ABD≌△AEM,可得BD=ME,根据BD=CD即可求得ME=CD,于是证得结论;
(3))如图2过点P作PQ⊥BE于Q,由角平分线的性质得到PA=PQ,再由三角形相似得到$\frac{AB}{EF}$=$\frac{AP}{PF}$,求得PF=3($\sqrt{2}$-1),得到PE,根据勾股定理列方程求解.
解答 解:(1)∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=$\frac{180°-30°}{2}$=75°,
∵DB=DC,∠DCB=30°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ABC-∠DBC=45°,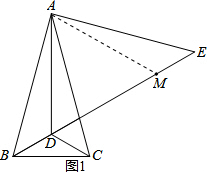
∵AB=AC,DB=DC,
∴AD所在直线垂直平分BC,
∴AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=15°,
∴∠ADE=∠ABD+∠BAD=60°;
(2)如图1,在线段DE上截取DM=AD,连接AM,
∵∠ADE=60°,DM=AD,
∴△ADM是等边三角形,
∴∠ADB=∠AME=120°
∵AE=AB,
∴∠ABD=∠E,
在△ABD和△AEM中,
$\left\{\begin{array}{l}{∠ADB=∠AME}\\{∠ABD=∠E}\\{AB=AE}\end{array}\right.$,
∴△ABD≌△AEM(AAS),
∴BD=ME,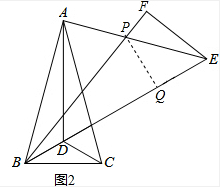
∵BD=CD,
∴CD=ME,
∵DE=DM+ME,
∴DE=AD+CD;
(3)如图2,过点P作PQ⊥BE于Q,
∵BP平分∠ABE,∠BAE=90°,
∴PA=PQ,
设PA=PQ=x,
∵∠AEB=45°,
∴PE=$\sqrt{2}$x,
∴AB=AE=AP+PE=($\sqrt{2}+$1)x,
∵EF⊥BP,
∴∠PFE=90°,
∴∠PFE=∠BAE,
∵∠APB=∠EPF,
∴△ABP∽△EFP,
∴$\frac{AB}{EF}$=$\frac{AP}{PF}$,
∴PF=3($\sqrt{2}$-1),
∴PE2=PF2+EF2=${[3(\sqrt{2}-1)]}^{2}$+32=${(\sqrt{2}x)}^{2}$,
解得:x=3$\sqrt{2-\sqrt{2}}$,
∴AB=3$\sqrt{2-\sqrt{2}}$•($\sqrt{2}$+1),
∴PB2=${[(3\sqrt{2-\sqrt{2}})•(\sqrt{2}+1)]}^{2}$+${(3\sqrt{2-\sqrt{2}})}^{2}$=36,
∴PB=6.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,相似三角形的判定和性质,勾股定理的应用,本题中求证△ABD≌△AEM是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
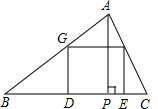 如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少?
如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 16 | 0.16 | 0.0016 | 1600 | 16000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
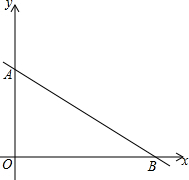 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按下列语句画出图形
按下列语句画出图形查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2,y=2 | B. | x=-2,y=2 | C. | x=-2,y=-2 | D. | x=2,y=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com