
| n | 16 | 0.16 | 0.0016 | 1600 | 16000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
分析 (1)从被开方数和算术平方根的小数点的移动位数考虑解答;
(2)根据(1)中的规律解答即可;
(3)根据(1)中的规律解答即可.
解答 解:(1)被开方数扩大或缩小102n倍,非负数的算术平方根就相应的扩大或缩小10n倍;
或者说成被开方数的小数点向左或向右移动2n位,算术平方根的小数点就向左或向右移动n位;
(2)$\sqrt{0.0206}≈0.1435$;$\sqrt{20600}≈143.5$;
(3)$\root{3}{2000}$≈12.60;
故答案为:(1)被开方数的小数点向左或向右每移动2位,算术平方根的小数点就相应向左或向右移动1位(2)0.1435;143.5;(3)12.60.
点评 本题考查了算术平方根,解题的关键在于从小数点的移动位数考虑.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
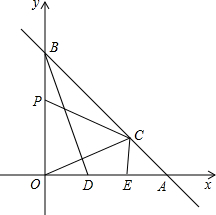 如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0
如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
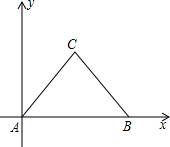 如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com