B
分析:根据等腰直角三角形的性质可得∠BAC=45°,再求出∠CAD=45°,从而得到∠BAC=∠CAD,然后利用“边角边”证明△ACD和△ACE全等,判定①正确;根据全等三角形对应边相等可得CD=CE,再求出∠CED=60°,得到△CDE为等边三角形,判定②正确;在等腰直角△ADE中,根据等腰三角形三线合一的性质可得AH⊥ED,即AC⊥ED,判定③正确;设EH=a,表示出AH、CH的长,从而得到AC的长,再根据等腰直角三角形的性质求出AE、AB,然后表示出BE的长,然后相比即可得到
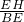
的值,判定④错误.
解答:∵∠BAD=90°,AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD-∠BAC=90°-45°=45°,
∴∠BAC=∠CAD,
在△ACD和△ACE中,
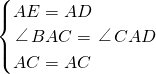
,
∴△ACD≌△ACE(SAS),故①正确;
∴CD=CE,
∵∠BCE=15°,
∴∠BEC=90°-∠BCE=90°-15°=75°,
∴∠CED=180°-∠BEC-∠AED=180°-75°-45°=60°,
∴△CDE为等边三角形,故②正确;
在△ADE中,∵AE=AD,∠BAC=∠CAD,
∴AH⊥ED,
即AC⊥ED,故③正确;
设EH=a,则AH=EH=a,CH=

EH=

a,
∴AC=a+

a,
根据等腰直角三角形的性质,AE=

EH=

a,
AB=

AC=

(a+

a)=
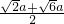
,
∴BE=AB-AE=
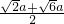
-

a=
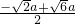
,
∴
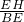
=
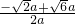
=
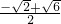
≠2,故④错误,
综上所述,正确的结论有①②③.
故选B.
点评:本题考查了直角梯形的性质,等腰直角三角形的性质,全等三角形的判定与性质,等边三角形的判定与性质,综合题但难度不大,熟记各性质是解题的关键.

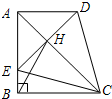 在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD,DE交对角线AC于点H,连接BH,有下列结论:
在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD,DE交对角线AC于点H,连接BH,有下列结论: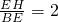
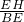 的值,判定④错误.
的值,判定④错误.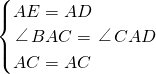 ,
, EH=
EH= a,
a, a,
a, EH=
EH= a,
a, AC=
AC= (a+
(a+ a)=
a)=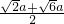 ,
,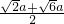 -
- a=
a=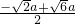 ,
,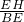 =
=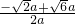 =
=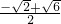 ≠2,故④错误,
≠2,故④错误,

 轻松暑假总复习系列答案
轻松暑假总复习系列答案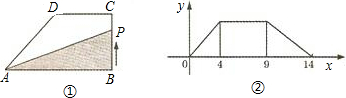
 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为