
【题目】水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价x(元/千克) | 400 | 250 | 240 | 200 | 150 | 125 | 120 | |
销售量y(千克) | 30 | 40 | 48 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式,并补全表格;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
【答案】(1)![]() ,表格中填:300,50;(2)20天(3)最高不超过每千克60元。.
,表格中填:300,50;(2)20天(3)最高不超过每千克60元。.
【解析】整体分析:
(1)根表格中x,y的对应值确定x,y的函数关系式,补全表格;(2)分别求出8天后剩余的产品数量及第8天的产品价格;(3)确定继续销售15天后的产品数量,求出后2天每天的销售量,即可求解.
(1)∵xy=12000,
∴反比例函数的解析式y=![]() .
.
当y=40时,x=![]() =300;
=300;
当x=240时y=![]() =50.
=50.
(2)销售8天后剩下的数量2104-(30+40+48+50+60+80+96+100)=1600,
当x=150时,y=![]() =80,
=80,
∴1600÷80=20天,
∴余下的这些海产品预计再用20天可以全部售出.
(3)1600-80×15=400千克,
400÷2=200千克/天,
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时,x=![]() =60.
=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.
【题型】解答题
【结束】
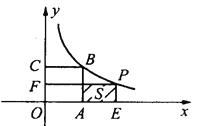
22
【题目】如图,已知正方形![]() 的面积为9,点
的面积为9,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 为其双曲线上的任一点,过点
为其双曲线上的任一点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,并设矩形
,并设矩形![]() 和正方形
和正方形![]() 不重合部分的面积为
不重合部分的面积为![]() .
.
(1)求![]() 点坐标和
点坐标和![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
【答案】(1) B(3,3); k=9 (2) ![]()
![]() (3) 当
(3) 当![]() ;当
;当![]()
【解析】整体分析:
(1)根据正方形的性质得OA,OC的长;(2)设P(m, ![]() ),分两种情况,当m≥3和0<m<3时,由矩形的面积列方程不解;(3)当m≥3和0<m<3时,分别用含m的代数式表示S.
),分两种情况,当m≥3和0<m<3时,由矩形的面积列方程不解;(3)当m≥3和0<m<3时,分别用含m的代数式表示S.
解:(1)因为正方形OABC的面积为9,
所以OA=OC=3,
所以B(3,3),
所以k=3×3=9.
(2)反比例函数的解析式为![]() ,
,
设P(m, ![]() ),
),
当m≥3时,AE=OE-OA=m-3,PE=![]() ,
,
S=AE×PE=(m-3)×![]() =
=![]() (m-3).
(m-3).
所以![]() (m-3)=
(m-3)=![]() ,
,
解得m=6, ![]() =
=![]() ,
,
即P(![]() );
);
当0<m<3时,AE=![]() -3,PE=m,
-3,PE=m,
S=AE×PE=(![]() -3)×m=m(
-3)×m=m(![]() -3).
-3).
所以m(![]() -3)=
-3)=![]() ,
,
解得m=![]() ,
, ![]() =6,
=6,
即P(![]() ).
).
则点P的坐标为(![]() )或(
)或(![]() ).
).
(3)当m≥3时,AE=OE-OA=m-3,PE=![]() ,
,
S=AE×PE=(m-3)×![]() =
=![]() (m-3)=9-
(m-3)=9-![]() ;
;
当0<m<3时,AE=![]() -3,PE=m,
-3,PE=m,
S=AE×PE=(![]() -3)×m=m(
-3)×m=m(![]() -3)=9-3m.
-3)=9-3m.
综上所述, 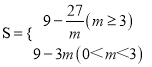 .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
![]()
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
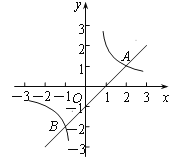
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组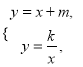 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 即可求得结果;
即可求得结果;
(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入![]() 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.
(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;
(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入![]() 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2
所以直线![]() 经过点B(-1,-2).
经过点B(-1,-2).
考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20
【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
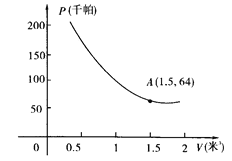
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com