
【题目】如图,点A、B、C在半径为9的⊙O上, 弧AB的长为2π , 则∠ACB的大小是.
【答案】20°
【解析】解答: 连结OA、OB.设∠AOB=n°.
∵ 弧AB的长为2π ,
∴ ![]() n×π×9
n×π×9
∴n=40,
∴∠AOB=40°,
∴∠ACB= ![]() ∠AOB=20°.
∠AOB=20°.
所以答案是20°.
连结OA、OB.先由弧AB的长为2π,利用弧长计算公式求出∠AOB=40°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半得到∠ACB= ![]() ∠AOB=20°.
∠AOB=20°.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握弧长计算公式(若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
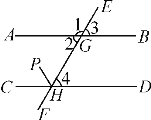
【题目】如图,直线AB,CD被EF所截,点G,H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠CHP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
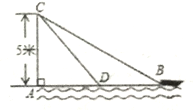
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,DE⊥AB于点E,DE = 4cm,∠A =45°,求菱形ABCD的面积和梯形DEBC的中位线长(精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个几何体由几个棱长均为1的小正方体搭成,从上面看到的几何体的形状图如图(1)所示,正方形中的数字表示该位置的小正方体的个数.
(1)请在图(2)的方格纸中画出从正面看和从左面看到的几何体的形状图;
(2)根据从三个方向看到的几何体的形状图,请你计算该几何体的表面积为________平方单位(包含底面);
(3)若从上面看到的几何体的形状图不变,几何体各位置的小正方体的个数可以改变,则搭成这样的几何体的表面积最大为________平方单位(包含底面).

图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价x(元/千克) | 400 | 250 | 240 | 200 | 150 | 125 | 120 | |
销售量y(千克) | 30 | 40 | 48 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式,并补全表格;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
【答案】(1)![]() ,表格中填:300,50;(2)20天(3)最高不超过每千克60元。.
,表格中填:300,50;(2)20天(3)最高不超过每千克60元。.
【解析】整体分析:
(1)根表格中x,y的对应值确定x,y的函数关系式,补全表格;(2)分别求出8天后剩余的产品数量及第8天的产品价格;(3)确定继续销售15天后的产品数量,求出后2天每天的销售量,即可求解.
(1)∵xy=12000,
∴反比例函数的解析式y=![]() .
.
当y=40时,x=![]() =300;
=300;
当x=240时y=![]() =50.
=50.
(2)销售8天后剩下的数量2104-(30+40+48+50+60+80+96+100)=1600,
当x=150时,y=![]() =80,
=80,
∴1600÷80=20天,
∴余下的这些海产品预计再用20天可以全部售出.
(3)1600-80×15=400千克,
400÷2=200千克/天,
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时,x=![]() =60.
=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.
【题型】解答题
【结束】
22
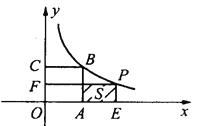
【题目】如图,已知正方形![]() 的面积为9,点
的面积为9,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 为其双曲线上的任一点,过点
为其双曲线上的任一点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,并设矩形
,并设矩形![]() 和正方形
和正方形![]() 不重合部分的面积为
不重合部分的面积为![]() .
.
(1)求![]() 点坐标和
点坐标和![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com