
【题目】问题提出
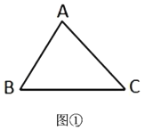
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为_________;
的周长为_________;

问题探究
(2)如图②,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积;
的面积;
问题解决.
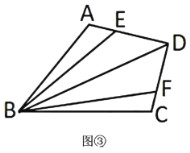
(3)如图③,某农业技术中心为新品种试验而修建了形状为四边形![]() 的试验田,
的试验田,![]() 、
、![]() 、
、![]() 是田间小路,点
是田间小路,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,其中道路
,其中道路![]() 的长度为100米,计划在四个三角形区域内种植不同的农作物,为及时了解农作物的生长情况,中心决定在点
的长度为100米,计划在四个三角形区域内种植不同的农作物,为及时了解农作物的生长情况,中心决定在点![]() 、
、![]() 处各架设监控器一台,
处各架设监控器一台,![]() 处的监控器的观察范围为
处的监控器的观察范围为![]() ,
,![]() 处的监控器的观察范围为
处的监控器的观察范围为![]() ,经测量,
,经测量,![]() ,
,![]() ,请探究四边形
,请探究四边形![]() 区域的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
区域的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)32:(3)
;(2)32:(3)![]()
【解析】
(1)过点A作AD⊥BC,将问题转化成解直角三角形问题,通过解直角三角形即可求出三角形三边的长,从而得出三角形的周长.
(2)通过将△BCD绕点B逆时针旋转90°得到△BAD1,构造出全等三角形,将求不规则四边形面积的问题转化成三角形面积问题.
(3)通过旋转构造△ABD≌△CBD1,作DH⊥BD1,得出DH的长,求出△BDD1的面积,根据已知条件求出∠BCD1=135°,推出当△DCD1的面积最大时,四边形BEDF的面积最小,而当C位于![]() 的中点时,CM最大,即△DCD1的面积最大,根据勾股定理求出OD=OC=OD1= 20
的中点时,CM最大,即△DCD1的面积最大,根据勾股定理求出OD=OC=OD1= 20![]() m及CM=(20
m及CM=(20![]() -20
-20![]() )m,从而得出△DCD1的面积,最后求出四边形
)m,从而得出△DCD1的面积,最后求出四边形![]() 的面积.
的面积.
解:(1)过点A作AD⊥BC于D
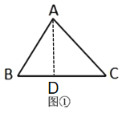
∴∠ADC=90°
∵∠C=45°,AC=3![]()
∴AD2+DC2=(3![]() )2,
)2,
∵∠C=45
∴AD=DC=3
∵∠B=60°
∴BD=![]() ,AB=
,AB=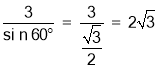
∴![]() 的周长=AB+BD+DC+AC=2
的周长=AB+BD+DC+AC=2![]() +
+![]() +3+3
+3+3![]() =
=![]()
(2)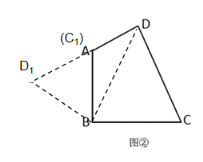
如图,将△BCD绕点B逆时针旋转90°,C点落在A点上,D点落在D1上
∴△BAD1≌△BCD
∴∠BAD1=∠C
∵∠BAD1+∠BAD=∠C+∠BAD=360-∠ADC-∠ABC=180°
∴D1,A,D三点共线
∵△BAD1≌△BCD
∴∠CBD=∠ABD1,BD1=BD=8
∴∠BAD1+∠ABD=∠BCD+∠ABD
即∠D1BD=∠ABC=90°
∴S四边形ABCD=S△ABD+S△BCD
= S△ABD+![]()
=![]()
=![]() BD
BD![]() BD1
BD1
=![]() ×8×8
×8×8
=32.
(3)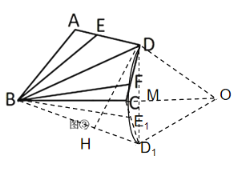
将△ABD以点B为旋转中心顺时针旋转,使点A旋转到点C,点D旋转到D1,点E旋转到点E1.
∴△ABD≌△CBD1
作DH⊥BD1,则BD=BD1=100m,∠ABC=∠DBD1
∵sin∠ABC=sin∠DBD1=0.8
∴DH=80m
∴![]() =4000m
=4000m
∵![]()
∴∠A+∠BCD=225°
∴∠BCD+∠BCD1=225°
∴∠BCD1=135°
当△DCD1的面积最大时,四边形BEDF的面积最小
∵△BDE≌△BD1E1
又DD1=![]() =40
=40![]() m
m
以DD1为弦,以DD1为底边的等腰直角三角形的顶点O为圆心画弧DD1,
DD1上任意一点和DD1构成的圆周角都是135°
∴当C位于![]() 的中点时,CM最大,即△DCD1的面积最大
的中点时,CM最大,即△DCD1的面积最大
∵△ODD1为等腰直角三角形,DD1=40![]() m
m
∴OD=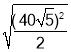 =20
=20![]() m
m
即OD=OC=OD1= 20![]() m
m
∴CM=(20![]() -20
-20![]() )m
)m
∴![]() =
=![]() ×40
×40![]() ×(20
×(20![]() -20
-20![]() )=(2000
)=(2000![]() -2000)m2
-2000)m2
∴S四边形BEDF=![]() ×[4000-(2000
×[4000-(2000![]() -2000)]=(
-2000)]=( ![]() )m2
)m2
故答案为(1)![]() ;(2)32;(3)
;(2)32;(3)![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.
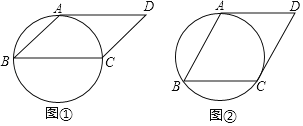
(1)若BC是圆的直径,画出平行四边形ABCD的边CD上的高;
(2)若CD与圆相切,画出平行四边形ABCD的边BC上的高AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
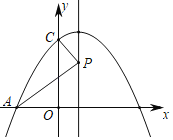
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解某小区家庭月均用水情况(单位:吨),随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
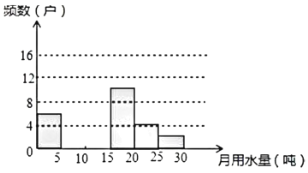
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有1000户家庭,根据调查数据估计,该小区月均有水量超过20吨的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
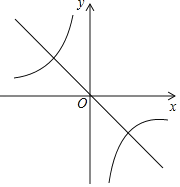
【题目】反比函数![]() 的图象如图所示.
的图象如图所示.
(1)求m的值;
(2)当x>﹣1时,y的取值范围是 ;
(3)当直线y2=﹣x与双曲线![]() 交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟的影响,2019年的猪肉价格创历史新高,同时其他肉类的价格也有一定程度的上涨,某超市11月份的猪肉销量是羊肉销量的![]() 倍,且猪肉价格为每千克
倍,且猪肉价格为每千克![]() 元羊肉价格为每千克
元羊肉价格为每千克![]() 元.
元.
(1)若该超市11月份猪肉、羊肉的总销售额不低于![]() 万元,则11月份的猪肉销量至少多少千克?
万元,则11月份的猪肉销量至少多少千克?
(2)12月份香肠腊肉等传统美食的制作,使得市场的猪肉需求加大,12月份猪肉的销量比11月份增长了![]() ,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了
,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了![]() ,羊肉的销量是11月份猪肉销量的
,羊肉的销量是11月份猪肉销量的![]() ,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了
,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了如下框中的题目:

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=”).
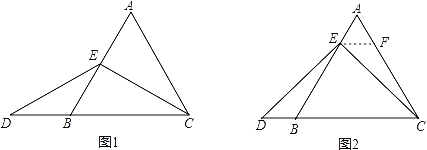
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com