
ЁОЬтФПЁПЪ§бЇПЮЩЯЃЌРЯЪІГіЪОСЫШчЯТПђжаЕФЬтФПЃК

аЁУєгыЭЌзРаЁДЯЬжТлКѓЃЌНјааСЫШчЯТНтД№ЃК
ЃЈ1ЃЉЬиЪтЧщПіЃЌЬНЫїНсТл
ЕБЕуEЮЊABЕФжаЕуЪБЃЌШчЭМ1ЃЌШЗЖЈЯпЖЮAEгыDBЕФДѓаЁЙиЯЕЃЎЧыФужБНгаДГіНсТлЃКAE_______DBЃЈЬюЁАЃОЁБЃЌЁАЃМЁБЛђЁАЃНЁБЃЉЃЎ
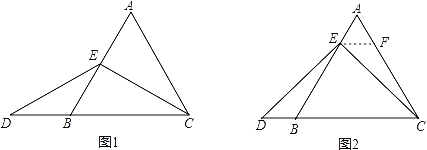
ЃЈ2ЃЉЬиР§ЦєЗЂЃЌНтД№ЬтФП
НтЃКЬтФПжаЃЌAEгыDBЕФДѓаЁЙиЯЕЪЧЃКAEЁЁ ЁЁDBЃЈЬюЁАЃОЁБЃЌЁАЃМЁБЛђЁАЃНЁБЃЉРэгЩШчЯТЃКШчЭМ2ЃЌЙ§ЕуEзїEFЁЮBCЃЌНЛACгкЕуFЃЌЃЈЧыФуНгзХМЬајЭъГЩвдЯТНтД№Й§ГЬЃЉ
ЃЈ3ЃЉЭиеЙНсТлЃЌЩшМЦаТЬт
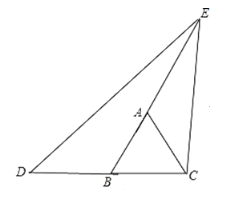
дкЕШБпШ§НЧаЮABCжаЃЌЕуEдкжБЯпЩЯABЩЯЃЌЕуDдкжБЯпBCЩЯЃЌЧвEDЃНECЃЎШєЁїABCЕФБпГЄЮЊ3ЃЌAEЃН5ЃЌЧѓCDЕФГЄЃЈЧыФужБНгаДГіНсЙћЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃНЃЛЃЈ2ЃЉЃНЃЌМћНтЮіЃЛЃЈ3ЃЉCDЕФГЄЪЧ8Лђ2
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪвдМАЕШБпШ§НЧаЮЕФаджЪПЩвдЕУГіЁЯBCE=ЁЯACE=30ЁуЃЌгжИљОнED=ECЕУЕНЁЯD=ЁЯECD=30ЁуЃЌПЩНјвЛВНЕУГіЁЯD=ЁЯDEBЃЌЭЦГіBD=BEМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉзїEFЁЮBCНЛACгкFЃЌЯШжЄУїЁїAEFЮЊЕШБпШ§НЧаЮЃЌдйжЄУїЁїDBEЁеЁїEFCМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЫФжжЧщаЮЃКЂйЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуDдкCBЕФбгГЄЯпЩЯЪБЃЌгЩЃЈ2ЃЉЭЌРэПЩЕУBD=AEЃЌдйИљОнCD=BD+BCМДПЩЧѓГіНсЙћЃЛЂкЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуDдкBCЕФбгГЄЯпЩЯЪБЃЌЙ§AзїANЁЭBCгкNЃЌЙ§EзїEMЁЭCDгкMЃЌЯШЧѓГіCMЕФГЄЃЌДгЖјПЩЕУГіCDЕФГЄЃЛЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуDдкBCЕФбгГЄЯпЩЯЪБЃЌгЩгкЁЯECDЃОЁЯEBCЃЌДЫЪБВЛДцдкECЃНEDЃЛЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуDдкCBЕФбгГЄЯпЩЯЪБЃЌгаЁЯECDЃОЁЯEDCЃЌДЫЪБЧщПіВЛДцдкЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌНсТлЃКAE=BDЃЎ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌAE=EBЃЌ
ЁрЁЯBCE=ЁЯACE=30ЁуЃЌЁЯABC=60ЁуЃЌ
ЁпED=ECЃЌ
ЁрЁЯD=ЁЯECD=30ЁуЃЌ
ЁпЁЯEBC=ЁЯD+ЁЯBEDЃЌ
ЁрЁЯD=ЁЯBED=30ЁуЃЌ
ЁрBD=BE=AEЃЎ
ЙЪД№АИЮЊЃК=ЃЎ
ЃЈ2ЃЉAEЃНDBЃЎ
РэгЩШчЯТЃКШчЭМ2ЃЌЙ§ЕуEзїEFЁЮBCЃЌНЛACгкЕуFЃЌ
дкЕШБпЁїABCжаЃЌЁЯABCЃНЁЯACBЃНЁЯBACЃН60ЁуЃЌABЃНBCЃНACЃЌ
ЁпEFЁЮBCЃЌ
ЁрЁЯAEFЃНЁЯABCЃЌЁЯAFEЃНЁЯACBЃЌ
ЁрЁЯAEFЃНЁЯAFEЃНЁЯBACЃН60ЁуЃЌ
ЁрAEЃНAFЃНEFЃЌ
ЁрABЉAEЃНACЉAFЃЌ
МДBEЃНCFЃЌ
ЁпЁЯABCЃНЁЯEDB+ЁЯBEDЃЌЁЯACBЃНЁЯECB+ЁЯFCEЃЌ
ЁпEDЃНECЃЌ
ЁрЁЯEDBЃНЁЯECBЃЌ
ЁрЁЯBEDЃНЁЯFCEЃЌ
дкЁїDBEКЭЁїEFCжа
 ЃЌ
ЃЌ
ЁрЁїDBEЁеЁїEFCЃЈSASЃЉЃЌ
ЁрDBЃНEFЃЌ
ЁрAEЃНBDЃЌ
ЙЪД№АИЮЊЃКЃНЃЎ
ЃЈ3ЃЉЗжЮЊЫФжжЧщПіЃК
ЂйЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуDдкCBЕФбгГЄЯпЩЯЪБЃЌШчЭМЃК
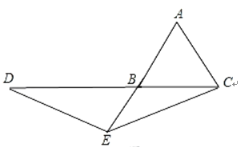
ЁпABЃНACЃН3ЃЌAEЃН5ЃЌ
ЭЌЃЈ2ЃЉПЩЕУBD=AEЃЌ
ЁрBDЃНAEЃН5ЃЌ
ЁрCDЃН3+5ЃН8ЃЛ
ЂкЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуDдкBCЕФбгГЄЯпЩЯЪБЃЌШчЭМЃЌЙ§AзїANЁЭBCгкNЃЌЙ§EзїEMЁЭCDгкMЃЌ
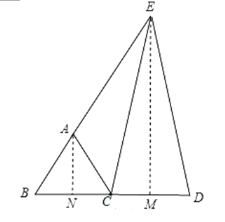
ЁпЕШБпШ§НЧаЮABCЃЌ
ЁрЁЯAEM=90Ёу-ЁЯB=30ЁуЃЌ
ЁрBMЃН![]() BEЃН
BEЃН![]() ЁСЃЈ3+5ЃЉЃН4ЃЌ
ЁСЃЈ3+5ЃЉЃН4ЃЌ
ЁрCMЃНBM-BCЃН4Љ3ЃН1ЃЌ
ЁпEC=EDЃЌEMЁЭCDЃЌ
ЁрCDЃН2CMЃН2ЃЛ
ЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуDдкBCЕФбгГЄЯпЩЯЪБЃЌШчЭМЃЌ
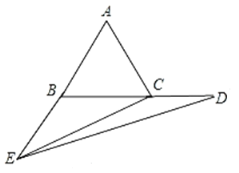
ЁпЁЯECDЃОЁЯEBCЃЈЁЯEBCЃН120ЁуЃЉЃЌЖјЁЯECDВЛФмДѓгк120ЁуЃЌЗёдђЁїEDCВЛЗћКЯШ§НЧаЮФкНЧКЭЖЈРэЃЌ
ЁрДЫЪБВЛДцдкECЃНEDЃЛ
ЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуDдкCBЕФбгГЄЯпЩЯЪБЃЌШчЭМЃЌ
ЁпЁЯEDCЃМЁЯABCЃЌЁЯECBЃОЁЯACBЃЌ
гжЁпЁЯABCЃНЁЯACBЃН60ЁуЃЌ
ЁрЁЯECDЃОЁЯEDCЃЌ
МДДЫЪБEDЁйECЃЌ
ЁрДЫЪБЧщПіВЛДцдкЃЌ
злЩЯЫљЪіЃКCDЕФГЄЪЧ8Лђ2ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬсГі
ЃЈ1ЃЉШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжмГЄЮЊ_________ЃЛ
ЕФжмГЄЮЊ_________ЃЛ

ЮЪЬтЬНОП
ЃЈ2ЃЉШчЭМЂкЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЮЪЬтНтОіЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌФГХЉвЕММЪѕжааФЮЊаТЦЗжжЪдбщЖјаоНЈСЫаЮзДЮЊЫФБпаЮ![]() ЕФЪдбщЬяЃЌ
ЕФЪдбщЬяЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЪЧЬяМфаЁТЗЃЌЕу
ЪЧЬяМфаЁТЗЃЌЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЦфжаЕРТЗ
ЃЌЦфжаЕРТЗ![]() ЕФГЄЖШЮЊ100УзЃЌМЦЛЎдкЫФИіШ§НЧаЮЧјгђФкжжжВВЛЭЌЕФХЉзїЮяЃЌЮЊМАЪБСЫНтХЉзїЮяЕФЩњГЄЧщПіЃЌжааФОіЖЈдкЕу
ЕФГЄЖШЮЊ100УзЃЌМЦЛЎдкЫФИіШ§НЧаЮЧјгђФкжжжВВЛЭЌЕФХЉзїЮяЃЌЮЊМАЪБСЫНтХЉзїЮяЕФЩњГЄЧщПіЃЌжааФОіЖЈдкЕу![]() ЁЂ
ЁЂ![]() ДІИїМмЩшМрПиЦївЛЬЈЃЌ
ДІИїМмЩшМрПиЦївЛЬЈЃЌ![]() ДІЕФМрПиЦїЕФЙлВьЗЖЮЇЮЊ
ДІЕФМрПиЦїЕФЙлВьЗЖЮЇЮЊ![]() ЃЌ
ЃЌ![]() ДІЕФМрПиЦїЕФЙлВьЗЖЮЇЮЊ
ДІЕФМрПиЦїЕФЙлВьЗЖЮЇЮЊ![]() ЃЌОВтСПЃЌ
ЃЌОВтСПЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧыЬНОПЫФБпаЮ
ЃЌЧыЬНОПЫФБпаЮ![]() ЧјгђЕФУцЛ§ЪЧЗёДцдкзюаЁжЕЃЌШєДцдкЃЌЧыЧѓГіЫќЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЧјгђЕФУцЛ§ЪЧЗёДцдкзюаЁжЕЃЌШєДцдкЃЌЧыЧѓГіЫќЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаУќЬтжаЃКЂйЙ§вЛЕугаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпЦНааЃЛЂкЦНЗНИљгыСЂЗНИљЯрЕШЕФЪ§га![]() КЭ
КЭ![]() ЃЛЂлдкЭЌвЛЦНУцФкЃЌШчЙћ
ЃЛЂлдкЭЌвЛЦНУцФкЃЌШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂмжБЯп
ЃЛЂмжБЯп![]() ЭтвЛЕу
ЭтвЛЕу![]() гыжБЯп
гыжБЯп![]() ЩЯИїЕуСЌНгЖјГЩЕФЫљгаЯпЖЮжаЃЌзюЖЬЯпЖЮЕФГЄЪЧ
ЩЯИїЕуСЌНгЖјГЩЕФЫљгаЯпЖЮжаЃЌзюЖЬЯпЖЮЕФГЄЪЧ![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЪЧ
ЕФОрРыЪЧ![]() ЃЛЂнЮоРэЪ§АќРЈе§ЮоРэЪ§ЁЂСуКЭИКЮоРэЪ§.ЦфжаецУќЬтЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЛЂнЮоРэЪ§АќРЈе§ЮоРэЪ§ЁЂСуКЭИКЮоРэЪ§.ЦфжаецУќЬтЕФИіЪ§ЪЧЃЈ ЃЉ
A. ![]() ИіB.
ИіB. ![]() ИіC.
ИіC. ![]() ИіD.
ИіD. ![]() Иі
Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCAЃНCBЃН4ЃЌСэгавЛПщЕШбќжБНЧШ§НЧАхЕФжБНЧЖЅЕуЗХдкCДІЃЌCPЃНCQЃН2ЃЌНЋШ§НЧАхCPQШЦЕуCа§зЊЃЈЕуPдкЁїABCФкВПЃЉЃЌСЌНгAPЁЂBPЁЂBQЃЎ

ЃЈ1ЃЉЧѓжЄЃКAPЃНBQЃЛ
ЃЈ2ЃЉЕБPQЁЭBQЪБЃЌЧѓAPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃК|Љ![]() |+ЃЈЉ1ЃЉ2019+2sin30Ёу+ЃЈ
|+ЃЈЉ1ЃЉ2019+2sin30Ёу+ЃЈ![]() ЃЉ0
ЃЉ0
ЃЈ2ЃЉНтЗНГЬЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯёНЛxжсгкЕуAЃЌНЛyжсгкЕуBЧвгыЗДБШР§КЏЪ§
ЕФЭМЯёНЛxжсгкЕуAЃЌНЛyжсгкЕуBЧвгыЗДБШР§КЏЪ§![]() (kЮЊГЃЪ§ЃЌkЁй0)ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЙ§ЕуCзї
(kЮЊГЃЪ§ЃЌkЁй0)ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЙ§ЕуCзї![]() жсгкMЃЌ
жсгкMЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЃЈ1ЃЉЧѓжБЯпABКЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉНсКЯЭМЯѓжБНгаДГіЃКЕБ![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫШЋСІПЙЛїаТаЭЙкзДВЁЖОИаШОЗЮбзЃЌМѕЩйЯрЛЅИаШОЃЌУПИіШЫГіУХЖМБиаыДјЩЯПкежЃЌЫљвдKN95аЭЕФПкежашЧѓСПдНРДдНДѓЃЎФГДѓаЭПкежЙЄГЇНгЕНЩњВњ200ЭђИБKN95аЭПкежЕФЩњВњШЮЮёЃЌМЦЛЎдкШєИЩЬьЭъГЩЃЌгЩгкЧщПівпЧщНєМБЃЌЙЄГЇШЋЬхВЛЮЗМшПрЃЌЙЄШЫШЋСІвдИАЃЌУПЬьБШдМЦЛЎЖрЩњВњ5ЭђИБПкежЃЌНсЙћжЛгУСЫдМЦЛЎЪБМфЕФ![]() ОЭдВТњЭъГЩЩњВњШЮЮёЃЌдђдМЦЛЎУПЬьЩњВњ_________ЭђИБПкежЃЎ
ОЭдВТњЭъГЩЩњВњШЮЮёЃЌдђдМЦЛЎУПЬьЩњВњ_________ЭђИБПкежЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌA(tЃЌ0)ЃЌB![]() ЃЌЖдгкЯпЖЮABКЭxжсЩЯЗНЕФЕуPИјГіШчЯТЖЈвхЃКЕБЁЯAPBЃН60ЁуЪБЃЌГЦЕуPЮЊABЕФЁАЕШНЧЕуЁБЃЎ
ЃЌЖдгкЯпЖЮABКЭxжсЩЯЗНЕФЕуPИјГіШчЯТЖЈвхЃКЕБЁЯAPBЃН60ЁуЪБЃЌГЦЕуPЮЊABЕФЁАЕШНЧЕуЁБЃЎ
(1)Шє![]() ЃЌдкЕуC(0ЃЌ
ЃЌдкЕуC(0ЃЌ![]() )ЃЌD
)ЃЌD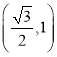 ЃЌE
ЃЌE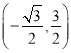 жаЃЌЯпЖЮABЕФЁАЕШНЧЕуЁБЪЧЁЁ ЁЁЃЛ
жаЃЌЯпЖЮABЕФЁАЕШНЧЕуЁБЪЧЁЁ ЁЁЃЛ
(2)жБЯпMNЗжБ№НЛxжсЁЂyжсгкЕуMЁЂNЃЌЕуMЕФзјБъЪЧ(6ЃЌ0)ЃЌЁЯOMNЃН30ЁуЃЎ
ЂйЯпЖЮABЕФЁАЕШНЧЕуЁБPдкжБЯпMNЩЯЃЌЧвЁЯABPЃН90ЁуЃЌЧѓЕуPЕФзјБъЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌЙ§ЕуBзїBQЁЭPAЃЌНЛMNгкЕуQЃЌЧѓЁЯAQBЕФЖШЪ§ЃЛ
ЂлШєЯпЖЮABЕФЫљгаЁАЕШНЧЕуЁБЖМдкЁїMONФкВПЃЌдђtЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃдкЪюМйЦкМфПЊеЙЁАаФЛГИаЖїЁЂаЂОДИИФИЁБЕФЪЕМљЛюЖЏЃЌГЋЕМбЇЩњдкМйЦкжаАяжњИИФИИЩМвЮёЃЌПЊбЇвдКѓЃЌаЃбЇЩњЛсЫцЛњГщШЁСЫВПЗжбЇЩњЃЌОЭЪюМйЁАЦНОљУПЬьАяжњИИФИИЩМвЮёЫљгУЪБГЄЁБНјааСЫЕїВщЃЌвдЯТЪЧИљОнЯрЙиЪ§ОнЛцжЦЕФЭГМЦЭМЃЎ
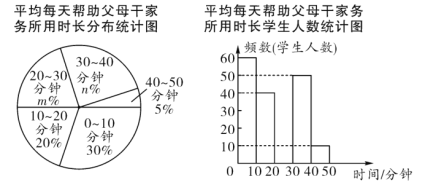
ИљОнЩЯЪіаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкБОДЮЫцЛњГщШЁЕФбљБОжаЃЌЕїВщЕФбЇЩњШЫЪ§ЮЊ______________ЃЎ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШчЙћИУаЃЙВгабЇЩњ1000ШЫЃЌБэФуЙРМЦЁАЦНОљУПЬьАяжњИИФИИЩМвЮёЫљгУЪБГЄВЛЩйгк30ЗжжгЁБЕФбЇЩњгаЖрЩйШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com