练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）计算：|﹣|+（﹣1）2019+2sin30°+（）0

    （2）解方程：

    【答案】（1）；（2）x=-3

    【解析】

    （1）利用绝对值代数意义、有理数的乘方、特殊角的三角函数值、零指数幂计算出各个数值，再运用实数的混合运算法则计算即可；

    （2）直接利用分式方程的解法解方程即可．

    解：（1）|﹣|+（﹣1）2019+2sin30°+（﹣）0

    ＝+（﹣1）+2×+1

    ＝+（﹣1）+1+1

    ＝

    （2）方程两边同乘以（x－2）得：x2＋2＋x－2＝6，

    则x2＋x－6＝0，

    （x－2）（x＋3）＝0，

    解得：x1＝2，x2＝﹣3，

    检验：当x＝2时，x－2＝0，故x＝2不是方程的根，

    当x＝﹣3时，x－2＝﹣3－2＝﹣5≠0

    故x＝﹣3是分式方程的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】九（1）班同学为了解某小区家庭月均用水情况（单位：吨），随机调查了该小区部分家庭，并将调查数据进行如下整理：

    月均用水量（吨）

    频数（户）

    频率

    6

    0.12

    0.24

    16

    0.32

    10

    0.20

    4

    25

    2

    0.04

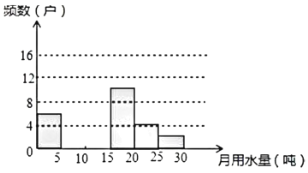
    请解答以下问题：

    （1）把上面的频数分布表和频数分布直方图补充完整；

    （2）若该小区有1000户家庭，根据调查数据估计，该小区月均有水量超过20吨的家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．

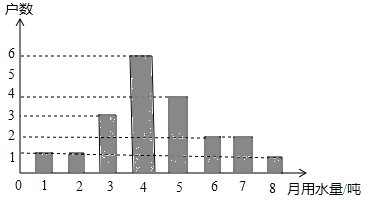
    （1）小明一共调查了多少户家庭？

    （2）所调查家庭5月份用水量的中位数、众数、平均数；

    （3）若该小区有400户居民，请你估计这个小区5月份的用水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．

    （1）求一次函数的表达式；

    （2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？

    （3）若该商场获得利润不低于500元，试确定销售单价的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知抛物线y＝x2﹣2x+b的顶点在x轴上，P（p，m），Q（q，m）（p＜q）是抛物线上的两点．

    （1）当m＝b时，求p，q的值；

    （2）将抛物线沿y轴平移，使得它与x轴的两个交点间的距离为4，试描述出这一变化过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，老师出示了如下框中的题目：

    小敏与同桌小聪讨论后，进行了如下解答：

    （1）特殊情况，探索结论

    当点E为AB的中点时，如图1，确定线段AE与DB的大小关系．请你直接写出结论：AE_______DB（填“＞”，“＜”或“＝”）．

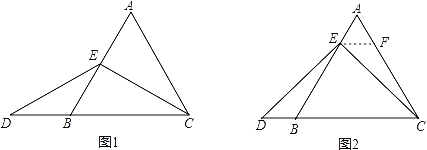
    （2）特例启发，解答题目

    解：题目中，AE与DB的大小关系是：AE　 　DB（填“＞”，“＜”或“＝”）理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你接着继续完成以下解答过程）

    （3）拓展结论，设计新题

    在等边三角形ABC中，点E在直线上AB上，点D在直线BC上，且ED＝EC．若△ABC的边长为3，AE＝5，求CD的长（请你直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市华润生活超市准备一次性购进A、B两种品牌的饮料100箱，此两种饮料每箱的进价和售价如下表所示设购进A种饮料x箱，且所购进的两种饮料能全部卖出，获得的总利润为y元．

    品牌

    A

    B

    进价元箱

    65

    49

    售价元箱

    80

    62

    求y关于x的函数关系式；

    由于资金周转原因，用于超市购进A、B两种饮料的总费用不超过5600元，并要求获得利润不低于1380元，则从两种饮料箱数上考虑，共有哪几种进货方案？利润售价进价

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，对角线AC，BD交于点O，过点B作BE⊥CD于点E，延长CD到点F，使DF=CE，连接AF.

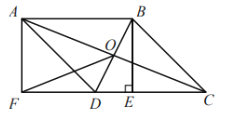
    (1)求证:四边形ABEF是矩形；

    (2)连接OF，若AB=6，DE=2，∠ADF=45°，求OF的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

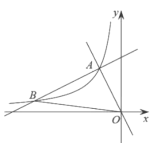
    【题目】如图，在平面直角坐标系中，一次函数和的图象相交于点，反比例函数的图象经过点.

    （1）求反比例函数的表达式；

    （2）设一次函数 的图象与反比例函数 的图象的另一个交点为，连接，求的面积.

    查看答案和解析>>

    同步练习册答案