
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2x+b的顶点在x轴上,P(p,m),Q(q,m)(p<q)是抛物线上的两点.
(1)当m=b时,求p,q的值;
(2)将抛物线沿y轴平移,使得它与x轴的两个交点间的距离为4,试描述出这一变化过程.
【答案】(1)p=0,q=2;(2)将原抛物线向下平移4个单位
【解析】
(1)根据题意求得b=1,可得出抛物线的解析式为y=x2﹣2x+1.由m=b=1,可得出关于x的一元二次方程,解之即可得出p、q的值;
(2)设平移后的抛物线为y=(x﹣1)2+k,由平移后的抛物线与x轴的两个交点的距离为4,可得出(3,0)是平移后的抛物线与x轴的一个交点,将其代入y=(x﹣1)2+k即可求出结论.
解:(1)∵抛物线y=x2﹣2x+b的顶点在x轴上,
∴![]() =0,
=0,
∴b=1.
∴抛物线的解析式为y=x2﹣2x+1.
∵m=b=1,
∴x2﹣2x+1=1,
解得:x1=0,x2=2,
∴p=0,q=2;
(2)设平移后的抛物线为y=(x﹣1)2+k.
∵抛物线的对称轴是x=1,平移后与x轴的两个交点之间的距离是4,
∴(3,0)是平移后的抛物线与x轴的一个交点,
∴(3﹣1)2+k=0,即k=﹣4,
∴变化过程是:将原抛物线向下平移4个单位.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】哈市红十字预计在2019年儿童节前为郊区某小学发放学习用品,联系某工厂加工学习用品.机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件,若加工1800件这样的产品,机器加工所用的时间是手工加工所用时间的![]() 倍.
倍.
(1)求手工每小时加工产品的数量;
(2)经过调查该小学的小学生的总数不超过1332名,每名小学生分发两个学习用品,工厂领导打算在两天内(48小时)完成任务,打算以机器加工为主,同时人工也参与加工(人工与机器加工不能同时进行),为了保证按时完成加工任务,人工至少要加工多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 为图形
为图形![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 直线
直线![]() 垂足为
垂足为![]() ,记
,记![]() 的长度为
的长度为![]() .
.
定义一:若![]() 存在最大值,则称其为“图形
存在最大值,则称其为“图形![]() 到直线
到直线![]() 的限距离”,记作
的限距离”,记作![]() ;
;
定义二:若![]() 存在最小值,则称其为“图形
存在最小值,则称其为“图形![]() 到直线
到直线![]() 的基距离”,记作
的基距离”,记作![]() ;
;
(1)已知直线![]() ,平面内反比例函数
,平面内反比例函数![]() 在第一象限内的图象记作
在第一象限内的图象记作![]() 则
则![]() .
.
(2)已知直线![]() ,点
,点![]() ,点
,点![]() 是
是![]() 轴上一个动点,
轴上一个动点,![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() 求此时
求此时![]() 的取值范围,
的取值范围,
(3)已知直线![]() 恒过定点
恒过定点![]() ,点
,点![]() 恒在直线
恒在直线![]() 上,点
上,点![]() 是平面上一动点,记以点
是平面上一动点,记以点![]() 为顶点,原点为对角线交点的正方形为图形
为顶点,原点为对角线交点的正方形为图形![]()
![]() ,若请直接写出
,若请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H.若AB=4,AE=![]() 时,则线段BH的长是 ;
时,则线段BH的长是 ;
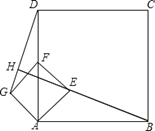
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() 与抛物线的另一个交点为,且
与抛物线的另一个交点为,且![]() .
.
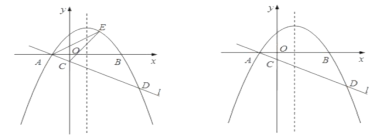
(1)直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() 用含
用含![]() 的式子表示);
的式子表示);
(2)点![]() 是直线
是直线![]() 上方的抛物线上的动点,若
上方的抛物线上的动点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
(1)通过配方将它写成![]() 的形式.
的形式.
(2)当![]() 时,函数有最 值,是 .
时,函数有最 值,是 .
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;)当
的增大而增大;)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
(4)该函数图象由![]() 的图象经过怎样的平移得到?
的图象经过怎样的平移得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=x(x﹣2)(0≤x≤2),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,得到图形.
(1)请写出抛物线C2的解析式:_____.
(2)若点P(4037.5,a)在图形G上,则a=_____.
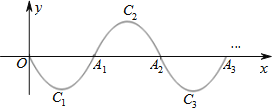
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(x1,y1)和点Q(x2,y2)是关于x的函数y=mx2﹣(2m+1)x+m+1(m为实数)图象上两个不同的点.对于下列说法:①不论m为何实数,关于x的方程mx2﹣(2m+1)x+m+1=0必有一个根为x=1;②当m=0时,(x1﹣x2)(y1﹣y2)<0成立;③当x1+x2=0时,若y1+y2=0,则m=﹣1;④当m≠0时,抛物线顶点在直线y=﹣![]() x+1上.其中正确的是( )
x+1上.其中正确的是( )
A.①②B.①②③C.③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com