
【题目】点P(x1,y1)和点Q(x2,y2)是关于x的函数y=mx2﹣(2m+1)x+m+1(m为实数)图象上两个不同的点.对于下列说法:①不论m为何实数,关于x的方程mx2﹣(2m+1)x+m+1=0必有一个根为x=1;②当m=0时,(x1﹣x2)(y1﹣y2)<0成立;③当x1+x2=0时,若y1+y2=0,则m=﹣1;④当m≠0时,抛物线顶点在直线y=﹣![]() x+1上.其中正确的是( )
x+1上.其中正确的是( )
A.①②B.①②③C.③④D.①②④
【答案】A
【解析】
根据方程解的定义对①进行判断;先得到当m=0时,函数解析式为y=﹣x+1,则可计算出![]() ,于是可根据非负数的性质对②进行判断;当m=﹣1时,解析式为
,于是可根据非负数的性质对②进行判断;当m=﹣1时,解析式为![]() ﹣
﹣![]() +
+![]() ,可计算出
,可计算出![]() +
+![]() =2
=2![]() ≠0,于是可对③进行判断;先计算出顶点坐标,然后根据一次函数图象上点的坐标特征对④进行判断.
≠0,于是可对③进行判断;先计算出顶点坐标,然后根据一次函数图象上点的坐标特征对④进行判断.
当x=1时,y=mx2﹣(2m+1)x+m+1=m﹣2m﹣1+m+1=0,
则方程mx2﹣(2m+1)x+m+1=0必有一个根为x=1,所以①正确;
当m=0时,y=﹣x+1,则y1=﹣x1+1,y2=﹣x2+1,
所以(x1﹣x2)(y1﹣y2)=(x1﹣x2)(﹣x1+x2)=﹣(x1﹣x2)2,
而点P(x1,y1)和点Q(x2,y2)是两个不同的点,
所以x1![]() x2,
x2,
则(x1﹣x2)(y1﹣y2)=﹣(x1﹣x2)2<0,所以②正确;
当m=﹣1时,y=﹣x2+x,
则y1=﹣x12+x1,y2=﹣x22+x2,
所以y1+y2=﹣x12+x1﹣x22+x2=﹣(x1+x2)2+2x1x2+(x1+x2),
当x1+x2=0时,
y1+y2=2x1x2≠0,所以③错误;
当m≠0时,顶点的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
当x=![]() 时,
时,![]() ,
,
所以抛物线的顶点不在直线![]() 上,所以④错误.
上,所以④错误.
综上:①②正确,
故选:A.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2x+b的顶点在x轴上,P(p,m),Q(q,m)(p<q)是抛物线上的两点.
(1)当m=b时,求p,q的值;
(2)将抛物线沿y轴平移,使得它与x轴的两个交点间的距离为4,试描述出这一变化过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作
的同侧作![]() 角的直角三角形
角的直角三角形![]() 和
和![]() 角的直角三角形
角的直角三角形![]() ,
,![]() 与
与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,连接
,连接![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③图中有5对相似三角形;④
;③图中有5对相似三角形;④![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )

A.1个B.2个C.4个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
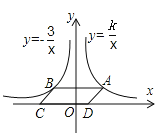
【题目】如图,点A是反比例函数y=![]() (x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣
(x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣![]() 的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,若SABCD=7,则k=__.
的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,若SABCD=7,则k=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
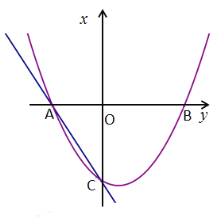
【题目】如图二次函数y=ax2+bx-2的图象交x轴于A(﹣1,0),B(2,0)两点,交y轴于点C,过A,C两点画直线.
(1)求二次函数的解析式;
(2)在平面直角坐标系中是否存在点D,使以A、B、C、D为顶点的四边形是平行四边形,如果存在,请直接写出点D的坐标,如果不存在,请说明理由。
(3)若点Q在AC下方的抛物线上运动,求以A、C、Q为顶点的三角形的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
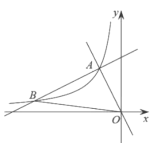
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
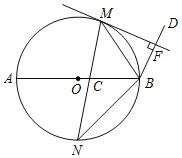
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
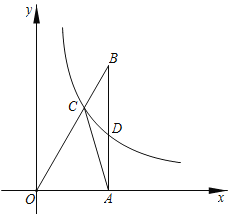
【题目】如图,在平面直角坐标系xOy中,Rt△OAB的直角顶点A在x轴上,∠B=30°,反比例函数y=![]() (k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4
(k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4![]() ,则实数k的值为( )
,则实数k的值为( )
A.4![]() B.6
B.6![]() C.8
C.8![]() D.10
D.10![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,双曲线
中,双曲线![]()
![]() 与直线
与直线![]()
![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 轴上一点.已知
轴上一点.已知![]() ,
,![]() 点坐标为
点坐标为![]() .
.
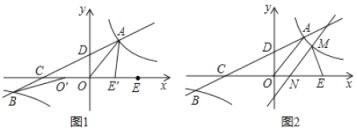
(1)将线段![]() 沿
沿![]() 轴平移得线段
轴平移得线段![]() (如图1),在移动过程中,是否存在某个位置使
(如图1),在移动过程中,是否存在某个位置使![]() 的值最大?若存在,求出
的值最大?若存在,求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
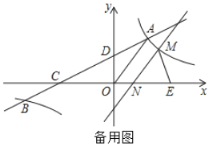
(2)将直线![]() 沿射线
沿射线![]() 平移,平移过程中交
平移,平移过程中交![]()
![]() 的图象于点
的图象于点![]() (
(![]() 不与
不与![]() 重合),交
重合),交![]() 轴于点
轴于点![]() (如图2).在平移过程中,是否存在某个位置使
(如图2).在平移过程中,是否存在某个位置使![]() 为以
为以![]() 为腰的等腰三角形?若存在,求出
为腰的等腰三角形?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com