
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作
的同侧作![]() 角的直角三角形
角的直角三角形![]() 和
和![]() 角的直角三角形
角的直角三角形![]() ,
,![]() 与
与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,连接
,连接![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③图中有5对相似三角形;④
;③图中有5对相似三角形;④![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )

A.1个B.2个C.4个D.3个
【答案】D
【解析】
如图,设AC与PB的交点为N,根据直角三角形的性质得到![]() ,根据相似三角形的判定定理得到△BAE∽△CAD,故①正确;根据相似三角形的性质得到∠BEA=∠CDA,推出△PME∽△AMD,根据相似三角形的性质得到MPMD=MAME,故②正确;由相似三角形的性质得到∠APM=∠DEM=90
,根据相似三角形的判定定理得到△BAE∽△CAD,故①正确;根据相似三角形的性质得到∠BEA=∠CDA,推出△PME∽△AMD,根据相似三角形的性质得到MPMD=MAME,故②正确;由相似三角形的性质得到∠APM=∠DEM=90![]() ,根据垂直的定义得到AP⊥CD,故④正确;同理:△APN∽△BCN,△PNC∽△ANB,于是得到图中相似三角形有6对,故③不正确.
,根据垂直的定义得到AP⊥CD,故④正确;同理:△APN∽△BCN,△PNC∽△ANB,于是得到图中相似三角形有6对,故③不正确.
如图,设AC与PB的交点为N,
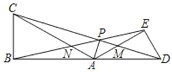
∵∠ABC=∠AED=90![]() ,∠BAC=∠DAE=30
,∠BAC=∠DAE=30![]() ,
,
∴![]() ,∠BAE=30
,∠BAE=30![]() +∠CAE,∠CAD=30
+∠CAE,∠CAD=30![]() +∠CAE,
+∠CAE,
∴∠BAE=∠CAD,
∴△BAE∽△CAD,故①正确;
∵△BAE∽△CAD,
∴∠BEA=∠CDA,
∵∠PME=∠AMD,
∴△PME∽△AMD,
∴![]() ,
,
∴MPMD=MAME,故②正确;
∴![]() ,
,
∵∠PMA=∠EMD,
∴△APM∽△DEM,
∴∠APM=∠DEM=90![]() ,
,
∴AP⊥CD,故④正确;
同理:△APN∽△BCN,△PNC∽△ANB,
∵△ABC∽△AED,
∴图中相似三角形有6对,故③不正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】点![]() 为图形
为图形![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 直线
直线![]() 垂足为
垂足为![]() ,记
,记![]() 的长度为
的长度为![]() .
.
定义一:若![]() 存在最大值,则称其为“图形
存在最大值,则称其为“图形![]() 到直线
到直线![]() 的限距离”,记作
的限距离”,记作![]() ;
;
定义二:若![]() 存在最小值,则称其为“图形
存在最小值,则称其为“图形![]() 到直线
到直线![]() 的基距离”,记作
的基距离”,记作![]() ;
;
(1)已知直线![]() ,平面内反比例函数
,平面内反比例函数![]() 在第一象限内的图象记作
在第一象限内的图象记作![]() 则
则![]() .
.
(2)已知直线![]() ,点
,点![]() ,点
,点![]() 是
是![]() 轴上一个动点,
轴上一个动点,![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() 求此时
求此时![]() 的取值范围,
的取值范围,
(3)已知直线![]() 恒过定点
恒过定点![]() ,点
,点![]() 恒在直线
恒在直线![]() 上,点
上,点![]() 是平面上一动点,记以点
是平面上一动点,记以点![]() 为顶点,原点为对角线交点的正方形为图形
为顶点,原点为对角线交点的正方形为图形![]()
![]() ,若请直接写出
,若请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
(1)通过配方将它写成![]() 的形式.
的形式.
(2)当![]() 时,函数有最 值,是 .
时,函数有最 值,是 .
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;)当
的增大而增大;)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
(4)该函数图象由![]() 的图象经过怎样的平移得到?
的图象经过怎样的平移得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
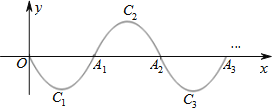
【题目】如图,一段抛物线:y=x(x﹣2)(0≤x≤2),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,得到图形.
(1)请写出抛物线C2的解析式:_____.
(2)若点P(4037.5,a)在图形G上,则a=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
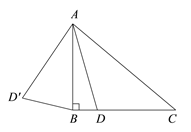
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,培养学生自主、团结协作能力,某校推出了以下四个项目供学生选择:![]() .家乡导游;
.家乡导游;![]() .艺术畅游;
.艺术畅游;![]() .体育世界;
.体育世界;![]() .博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目.学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解答下列问题:
.博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目.学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解答下列问题:
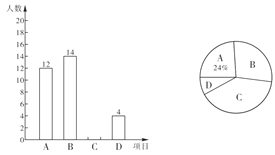
(1)该班学生总人数是______人;
(2)将条形统计图补充完整,并求![]() 项目所在扇形的圆心角的度数;
项目所在扇形的圆心角的度数;
(3)老师发现报名参加“博物旅行”的学生中恰好有两名男生,现准备从这些参加“博物旅行”的学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作。《九章算术》中记载:“今有五省、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平。并燕、雀重一斤。问燕,雀一枚各重几何?”译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(x1,y1)和点Q(x2,y2)是关于x的函数y=mx2﹣(2m+1)x+m+1(m为实数)图象上两个不同的点.对于下列说法:①不论m为何实数,关于x的方程mx2﹣(2m+1)x+m+1=0必有一个根为x=1;②当m=0时,(x1﹣x2)(y1﹣y2)<0成立;③当x1+x2=0时,若y1+y2=0,则m=﹣1;④当m≠0时,抛物线顶点在直线y=﹣![]() x+1上.其中正确的是( )
x+1上.其中正确的是( )
A.①②B.①②③C.③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
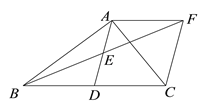
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com