练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作。《九章算术》中记载:“今有五省、六燕，集称之衡，雀俱重，燕俱轻，一雀一燕交而处，衡适平。并燕、雀重一斤。问燕，雀一枚各重几何?”译文:“今有只雀、只燕，分别聚集而且用衡器称之，聚在一起的雀重，燕轻.将一只雀、一只燕交换位置而放，重量相等.只雀、只燕重量为斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)

    【答案】雀、燕每1只各重 斤、斤．

    【解析】

    设雀、燕每只各重x斤、y斤，根据等量关系：今有5只雀、6只燕，分别聚集而且用衡器称之，聚在一起的雀重，燕轻．将一只雀、一只燕交换位置而放，重量相等．5只雀、6只燕重量为1斤，列出方程组求解即可．

    解：设雀、燕每只各重x斤、y斤，
    由题意得，，解得：，
    答：雀、燕每只各重 斤、斤．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，点E在正方形的边上（不与点B，C重合），是对角线，延长到点F，使，过点E作的垂线，垂足为G，连接，．

    （1）根据题意补全图形，并证明；

    （2）①用等式表示线段与的数量关系，并证明；

    ②用等式表示线段，，之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“数学运算”是数学学科核心素养之一，某校对七年级学生“数学运算能力”情况进行调研，从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析，成绩分为A、B、C三个层次，绘制了频数分布表（如下），请根据图表信息解答下列问题：

    （1）补全频数分布；

    （2）如果成绩为A等级的同学属于优秀，请你估计该校七年级约有多少人达到优秀水平？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OC平分∠MON，P为OC上一点，PA⊥OM，PB⊥ON，垂足分别为A、B，连接AB，得到以下结论：（1）PA=PB；（2）OA=OB；（3）OP与AB互相垂直平分；（4）OP平分∠APB，正确的个数是（　　）

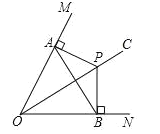
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．

    探究一：如图1．在△ABC中，已知O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现．理由如下：

    ∵BO和CO分别是∠ABC与∠ACB的平分线，

    ∴，；

    ∴，

    ∴

    （1）探究二：如图2中，已知O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？并说明理由．

    （2）探究二：如图3中，已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区举行“互联网+”征文比赛，已知每篇参赛征文成绩记分，组委会从篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表：

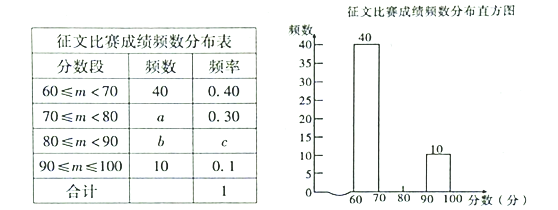
    请根据以上信息，解决下列问题：

    （1）征文比赛成绩频数分布表中的值是 ；

    （2）请求出的值，再补全征文比赛成绩频数分布直方图；

    （3）若绘制扇形统计图，分别计算分数段，所对应扇形的圆心角度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

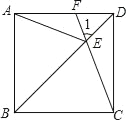
    【题目】如图，在正方形ABCD中，E是对角线BD上任意一点（BE＞DE），CE的延长线交AD于点F，连接AE．

    （1）求证：△ABE∽△FDE；

    （2）当BE=3DE时，求tan∠1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情景：如图1,AB∥CD,∠PAB=130°,∠PCD=120°，求∠APC的度数.

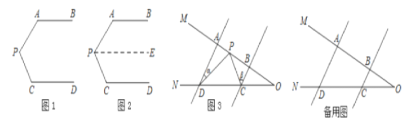
    (1)天天同学看过图形后立即口答出：∠APC=110°，请你补全他的推理依据.

    如图2,过点P作PE∥AB，

    ∵AB∥CD，

    ∴PE∥AB∥CD.(___)

    ∴∠A+∠APE=180°.

    ∠C+∠CPE=180°.(___)

    ∵∠PAB=130°,∠PCD=120°，

    ∴∠APE=50°,∠CPE=60°

    ∴∠APC=∠APE+∠CPE=110°.(___)

    问题迁移：

    (2)如图3,AD∥BC，当点P在A. B两点之间运动时，∠ADP=∠α，∠BCP=∠β，求∠CPD与∠α、∠β之间有何数量关系?请说明理由。

    (3)在(2)的条件下,如果点P在A. B两点外侧运动时(点P与点A. B. O三点不重合)，请你直接写出∠CPD与∠α、∠β之间的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)操作发现：

    如图①'在正方形ABCD中，过A点有直线AP，点B关于AP的对称点为E，连接DE交AP于点F,当∠BAP=20°时，则∠AFD= °；当∠BAP=α°(0<α<45°)时，则∠AFD= °；猜想线段DF, EF, AF之间的数量关系：DF-EF= AF（填系数）；

    (2)数学思考：

    如图②,若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=120°”，其他条件不变，则∠AFD= °；线段DF, EF, AF之间的数量关系是否发生改变，若发生改变，请写出数量关系并说明理由；

    (3)类比探究：

    如图③，若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=α°”，其他条件不变，则∠AFD= °；请直接写出线段DF,EF,AF之间的数量关系： .

    查看答案和解析>>

    同步练习册答案