
【题目】已知,点E在正方形![]() 的
的![]() 边上(不与点B,C重合),
边上(不与点B,C重合),![]() 是对角线,延长
是对角线,延长![]() 到点F,使
到点F,使![]() ,过点E作
,过点E作![]() 的垂线,垂足为G,连接
的垂线,垂足为G,连接![]() ,
,![]() .
.

(1)根据题意补全图形,并证明![]() ;
;
(2)①用等式表示线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
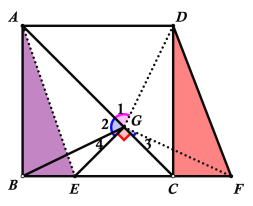
(1)补全图形后,如下图所示,证明△EGC为等腰三角形即可;
(2)①连接GF,GD,证明△BGE≌△FGC,得到GF=GB,再证明△ABG≌△ADG,得到GD=GF,进一步得到△DGF为等腰直角三角形,进而得到![]() ;
;
②连接AE,证明△ABE≌△DCF,得到DF=AE,在Rt△AEG中由勾股定理得到![]() ,进而得到
,进而得到![]() .
.
解:(1)补全图形如下所示:
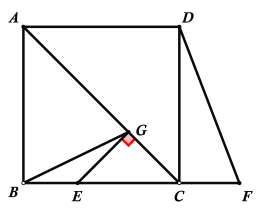
证明:∵四边形ABCD为正方形,AC是对角线
∴∠GCE=45°
∵EG⊥AC
∴∠EGC=90°
∴∠GEC=∠GCE=45°
∴△GEC为等腰直角三角形
∴GC=GE.
(2)①连接GF,GD,如下图所示:
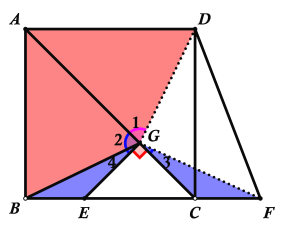
由(1)知:∠GEB=180°-∠GEC=180°-45°=135°,∠GCF=180°-∠GCE=180°-45°=135°
∴∠GEB=∠GCF
在△GBE和△GCF中
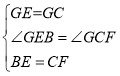 ,∴△GBE≌△GCF(SAS)
,∴△GBE≌△GCF(SAS)
∴GF=GB,且∠3=∠4
在△ABG和△ADG中
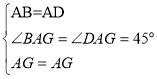 ,∴△ABG≌△ADG(SAS)
,∴△ABG≌△ADG(SAS)
∴GB=GD,∠1=∠2
故GF=GD,△GDF为等腰三角形
又∠2+∠4=90°
∴∠1+∠3=90°,即∠DGF=90°
∴△GDF为等腰直角三角形
∴![]() .
.
故答案为:![]() .
.
②连接AE,如下图所示:
在△ABE和△DCF中
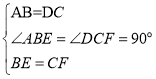 ,∴△ABE≌△DCF(SAS)
,∴△ABE≌△DCF(SAS)
∴![]()
又由①中知:![]()
∴![]()
且![]()
在Rt△AGE中,由勾股定理:![]() ,将上述等式代入:
,将上述等式代入:
故有![]()
即:![]() .
.
故线段![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福州电信公司开设了A、B两种市内移动通信业务:A种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.1元;B种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,A、B两种的费用分别为![]() 和
和![]() 元.
元.
(1)试分别写出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(2)每月通话时间为多长时,开通A种业务和B种业务费用一样.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
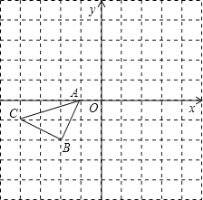
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△AB1C1关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将1、![]() 、
、![]() 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )

A.1B.2C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
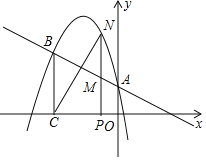
【题目】如图所示,二次函数y=ax2﹣![]() x+c的图象经过点A(0,1),B(﹣3,
x+c的图象经过点A(0,1),B(﹣3, ![]() ),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
),A点在y轴上,过点B作BC⊥x轴,垂足为点C.
(1)求直线AB的解析式和二次函数的解析式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)点N是二次函数图象上一点(点N在AB上方),是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作。《九章算术》中记载:“今有五省、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平。并燕、雀重一斤。问燕,雀一枚各重几何?”译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
斤。问雀、燕每只各重多少斤?”(每只雀的重量相同、每只燕的重量相同)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com