
【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
分别假设出白天的单价为每度a元,晚间的单价比白天低的百分数为x,可以表示出晚间的单价,这样可以表示出5,6月份的白天与晚间电费,即可列出方程,求出未知数即可.
设白天的单价为每度a元,晚间的单价比白天低的百分数为x,
即晚间的单价为每度(1x)a元,又设5月份晚间用电量为n度,则:
5月份白天用电量为:(1+50%)=1.5n度,
5月份电费为:1.5na+(1x)na=(2.5x)na元,
6月份白天用电量为:1.5n(160%)=0.6n度,
6月份晚间用电量为:(n+1.5n)(1+20%)0.6n=2.4n度,
6月份电费为:0.6na+2.4(1x)na=(32.4x)na元,
根据题意得:(32.4x)na=(2.5x)(110%)na.
整理得:1.5x=0.75,
解得:x=0.5=50%.
故选:B.


科目:初中数学 来源: 题型:
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 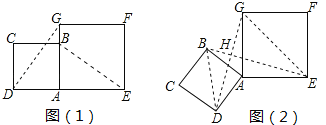
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
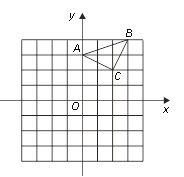
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点E在正方形![]() 的
的![]() 边上(不与点B,C重合),
边上(不与点B,C重合),![]() 是对角线,延长
是对角线,延长![]() 到点F,使
到点F,使![]() ,过点E作
,过点E作![]() 的垂线,垂足为G,连接
的垂线,垂足为G,连接![]() ,
,![]() .
.

(1)根据题意补全图形,并证明![]() ;
;
(2)①用等式表示线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对![]() 岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
请根据图中的信息,解决下列问题:
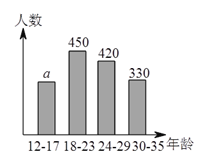
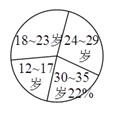
(![]() )求条形统计图中
)求条形统计图中![]() 的值.
的值.
(![]() )求扇形统计图中
)求扇形统计图中![]() 岁部分所占的百分比;
岁部分所占的百分比;
(![]() )据报道,目前我国
)据报道,目前我国![]() 岁网瘾人数约为
岁网瘾人数约为![]() 万,请估计其中
万,请估计其中![]() 岁的人数.
岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
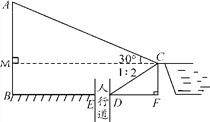
【题目】城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1.在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现![]() .理由如下:
.理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴![]() ,
,![]() ;
;
∴![]() ,
,
∴![]()

(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com