
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 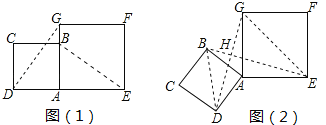
【答案】6
【解析】试题分析:)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,AG=AE,∠DAB=∠EAG=90°,
∴∠DAB+∠BAG =∠EAG+∠BAG,
∴∠DAG=∠BAE,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
在正方形AEFG中,∠AGE=∠AEG=45°,
∴∠HGE+∠HEG=45°+∠AGD+45°-∠AEB=90°,
所以∠GHE=90°,
所以对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;
同理对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,
∴△GHE和△BHD面积之和的最大值为: ![]() ×22+
×22+![]() ×(2
×(2![]() )2=2+4=6.
)2=2+4=6.
故答案为6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
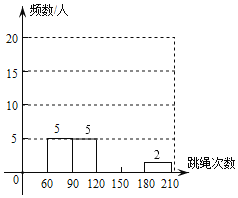
【题目】学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如下不完整统计图表,请根据图表中的信息解答下列问题.
组别 | 次数 | 频数(人) | 百分比 |
1 | 60≤x<90 | 5 | 10% |
2 | 90≤x<120 | 5 | b |
3 | 120≤x<150 | 18 | 36% |
4 | 150≤x<180 | a | c |
5 | 180≤x<210 | 2 | 4% |
合计 | 50 | 1 | |
(1)直接写出a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?(
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A顺时针旋转90°,得到线段AE,连接DE.

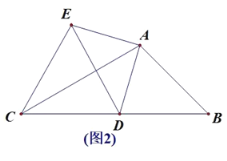
(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.
(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.
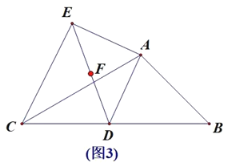
(3)如图3,点F为线段DE中点,AB=![]() ,求出动点D从B运动到C,点F经过的路径长度.
,求出动点D从B运动到C,点F经过的路径长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
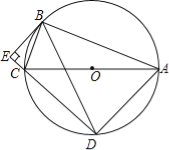
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
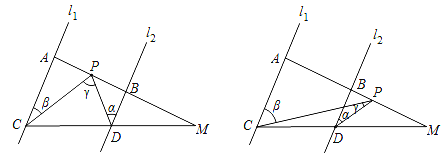
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③ 2a+b=0;④b2-4ac>0 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有()

A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
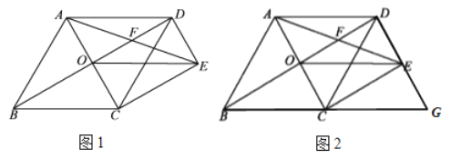
(1)求证:![]() ;
;
(2)如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形
,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形![]() 和四边形
和四边形![]() 外)
外)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com