
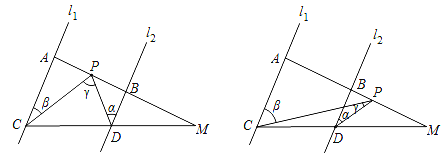
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
科目:初中数学 来源: 题型:
【题目】如图,动点 P 在平面直角坐标系中按图中箭头所示方向运动,第 1 次从原点运动到点(1,1),第 2 次接着运动到点(2,0),第 3 次接着运动到点(3,2),……,按这样的运动规律,经过第2025 次运动后,动点 P 的坐标是( )
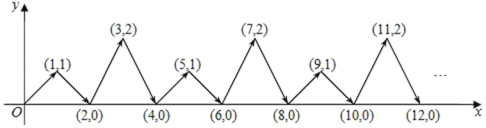
A.(2025,1)B.(2025,0)C.(2026,2)D.(2026,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出不等式kx+b﹣![]() >0的解集;
>0的解集;
(3)求△AOB的面积;
(4)若点P在x轴上、点Q在y轴上,且以P、Q、A、B为顶点的四边形是平行四边形,请直接写出点P、Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,对于下列结论:①△ABE≌△CDF;②AM=MN=NC;③EM=![]() BM,④S△ABM=S△AME,其中正确的有( )
BM,④S△ABM=S△AME,其中正确的有( )
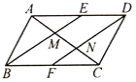
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 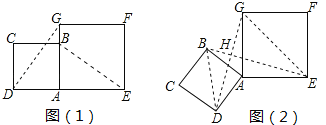
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,C、D两点分别从P、B出发以1cm/s、2 cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置: ![]()
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求![]() 的值。
的值。
![]()
(3)在(1)的条件下,若C、D运动5秒后,恰好有![]() ,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②![]() 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点E在正方形![]() 的
的![]() 边上(不与点B,C重合),
边上(不与点B,C重合),![]() 是对角线,延长
是对角线,延长![]() 到点F,使
到点F,使![]() ,过点E作
,过点E作![]() 的垂线,垂足为G,连接
的垂线,垂足为G,连接![]() ,
,![]() .
.

(1)根据题意补全图形,并证明![]() ;
;
(2)①用等式表示线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com