
ЁОЬтФПЁПШчЭМЃЌPЪЧЯпЖЮABЩЯвЛЕуЃЌCЁЂDСНЕуЗжБ№ДгPЁЂBГіЗЂвд1cm/sЁЂ2 cm/sЕФЫйЖШбижБЯпABЯђзѓдЫЖЏЃЈCдкЯпЖЮAPЩЯЃЌDдкЯпЖЮBPЩЯЃЉ
(1)ШєCЁЂDдЫЖЏЕНШЮвЛЪБПЬЪБЃЌзмгаPDЃН2ACЃЌЧыЫЕУїPЕудкЯпЖЮABЩЯЕФЮЛжУЃК ![]()
(2)дк(1)ЕФЬѕМўЯТЃЌQЪЧжБЯпABЩЯвЛЕуЃЌЧвAQЃBQ=PQЃЌЧѓ![]() ЕФжЕЁЃ
ЕФжЕЁЃ
![]()
(3)дк(1)ЕФЬѕМўЯТЃЌШєCЁЂDдЫЖЏ5УыКѓЃЌЧЁКУга![]() ЃЌДЫЪБCЕуЭЃжЙдЫЖЏЃЌDЕуМЬајдЫЖЏЃЈDЕудкЯпЖЮPBЩЯЃЉЃЌMЁЂNЗжБ№ЪЧCDЁЂPDЕФжаЕуЃЌЯТСаНсТлЃКЂйPMЃPNЕФжЕВЛБфЃЛЂк
ЃЌДЫЪБCЕуЭЃжЙдЫЖЏЃЌDЕуМЬајдЫЖЏЃЈDЕудкЯпЖЮPBЩЯЃЉЃЌMЁЂNЗжБ№ЪЧCDЁЂPDЕФжаЕуЃЌЯТСаНсТлЃКЂйPMЃPNЕФжЕВЛБфЃЛЂк![]() ЕФжЕВЛБфЃЌПЩвдЫЕУїЃЌжЛгавЛИіНсТлЪЧе§ШЗЕФЃЌЧыФуевГіе§ШЗЕФНсТлВЂЧѓжЕ.
ЕФжЕВЛБфЃЌПЩвдЫЕУїЃЌжЛгавЛИіНсТлЪЧе§ШЗЕФЃЌЧыФуевГіе§ШЗЕФНсТлВЂЧѓжЕ.
ЁОД№АИЁПЃЈ1ЃЉЕуPдкЯпЖЮABЩЯЕФ![]() ДІЃЛЃЈ2ЃЉ
ДІЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂк
ЃЛЃЈ3ЃЉЂк![]() ЕФжЕВЛБф.
ЕФжЕВЛБф.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнCЁЂDЕФдЫЖЏЫйЖШжЊBD=2PCЃЌдйгЩвбжЊЬѕМўPD=2ACЧѓЕУPB=2APЃЌЫљвдЕуPдкЯпЖЮABЩЯЕФ![]() ДІЃЛ
ДІЃЛ
ЃЈ2ЃЉгЩЬтЩшЛГіЭМЪОЃЌИљОнAQ-BQ=PQЧѓЕУAQ=PQ+BQЃЛШЛКѓЧѓЕУAP=BQЃЌДгЖјЧѓЕУPQгыABЕФЙиЯЕЃЛ
ЃЈ3ЃЉЕБЕуCЭЃжЙдЫЖЏЪБЃЌгаCDЃН![]() ABЃЌДгЖјЧѓЕУCMгыABЕФЪ§СПЙиЯЕЃЛШЛКѓЧѓЕУвдABБэЪОЕФPMгыPNЕФжЕЃЌЫљвдMNЃНPNPMЃН
ABЃЌДгЖјЧѓЕУCMгыABЕФЪ§СПЙиЯЕЃЛШЛКѓЧѓЕУвдABБэЪОЕФPMгыPNЕФжЕЃЌЫљвдMNЃНPNPMЃН![]() ABЃЎ
ABЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЃКBD=2PC
ЁпPD=2ACЃЌ
ЁрBD+PD=2ЃЈPC+ACЃЉЃЌМДPB=2AP.
ЁрЕуPдкЯпЖЮABЩЯЕФ![]() ДІЃЛ
ДІЃЛ
ЃЈ2ЃЉШчЭМЃК
![]()
ЁпAQ-BQ=PQЃЌ
ЁрAQ=PQ+BQЃЌ
ЁпAQ=AP+PQЃЌ
ЁрAP=BQЃЌ
ЁрPQ=![]() ABЃЌ
ABЃЌ
Ёр![]()
ЃЈ3ЃЉЂк![]() ЕФжЕВЛБф.
ЕФжЕВЛБф.
РэгЩЃКШчЭМЃЌ
![]()
ЕБЕуCЭЃжЙдЫЖЏЪБЃЌгаCD=![]() ABЃЌ
ABЃЌ
ЁрCM=![]() ABЃЌ
ABЃЌ
ЁрPM=CM-CP=![]() AB-5ЃЌ
AB-5ЃЌ
ЁпPD=![]() AB-10ЃЌ
AB-10ЃЌ
ЁрPN=![]() AB-10ЃЉ=
AB-10ЃЉ=![]() AB-5ЃЌ
AB-5ЃЌ
ЁрMN=PN-PM=![]() ABЃЌ
ABЃЌ
ЕБЕуCЭЃжЙдЫЖЏЃЌDЕуМЬајдЫЖЏЪБЃЌMNЕФжЕВЛБфЃЌ
Ыљвд![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊЬсГЋНкдМгУЫЎЃЌзМБИЪЕааздРДЫЎЁАНзЬнМЦЗбЁБЗНЪНЃЌгУЛЇгУЫЎВЛГЌГіЛљБОгУЫЎСПЕФВПЗжЯэЪмЛљБОМлИёЃЌГЌГіЛљБОгУЫЎСПЕФВПЗжЪЕааГЌМлЪеЗбЃЌЮЊИќКУЕФОіВпЃЌздРДЫЎЙЋЫОЫцЛњГщШЁСЫВПЗжгУЛЇЕФгУЫЎСПЪ§ОнЃЌВЂЛцжЦСЫШчЭМВЛЭъећЕФЭГМЦЭМЃЌЃЈУПзщЪ§ОнАќРЈдкгвЖЫЕуЕЋВЛАќРЈзѓЖЫЕуЃЉЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
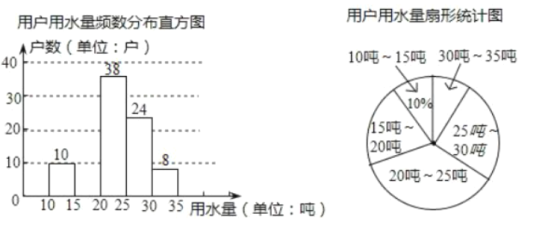
ЃЈ1ЃЉДЫДЮГщбљЕїВщЕФбљБОШнСПЪЧ ЃЎ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЌЧѓЩШаЮЭМжаЁА![]() ЖжЁЊ
ЖжЁЊ![]() ЖжЁБВПЗжЕФдВаФНЧЕФЖШЪ§.
ЖжЁБВПЗжЕФдВаФНЧЕФЖШЪ§.
ЃЈ3ЃЉШчЙћздРДЫЎЙЋЫОНЋЛљБОгУЫЎСПЖЈЮЊУПЛЇ![]() ЖжЃЌФЧУДИУЕиЧј
ЖжЃЌФЧУДИУЕиЧј![]() ЭђгУЛЇжадМгаЖрЩйгУЛЇЕФгУЫЎШЋВПЯэЪмЛљБОМлИёЃП
ЭђгУЛЇжадМгаЖрЩйгУЛЇЕФгУЫЎШЋВПЯэЪмЛљБОМлИёЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
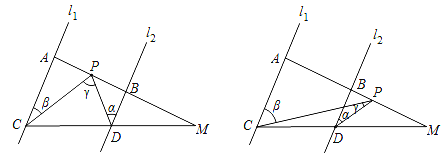
ЁОЬтФПЁПШчЭМЃЌвбжЊl1ЁЮl2ЃЌЯпЖЮMAЗжБ№гыжБЯпl1ЃЌl2НЛгкЕуAЃЌBЃЌЯпЖЮMCЗжБ№гыжБЯпl1ЃЌl2НЛгкЕуCЃЌDЃЌЕуPдкЯпЖЮAMЩЯдЫЖЏЃЈPЕугыAЃЌBЃЌMШ§ЕуВЛжиКЯЃЉЃЌЩшЁЯPDBЃНІСЃЌЁЯPCAЃНІТЃЌЁЯCPDЃНІУЃЎ
ЃЈ1ЃЉШєЕуPдкAЃЌBСНЕужЎМфдЫЖЏЪБЃЌШєaЃН25ЁуЃЌІТЃН40ЁуЃЌФЧУДІУЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєЕуPдкAЃЌBСНЕужЎМфдЫЖЏЪБЃЌЬНОПІСЃЌІТЃЌІУжЎМфЕФЪ§СПЙиЯЕЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуPдкBЃЌMСНЕужЎМфдЫЖЏЪБЃЌІСЃЌІТЃЌІУжЎМфгаКЮЪ§СПЙиЯЕЃПЃЈжЛашжБНгаДГіНсТлЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯФМОЪЧДЙЕіЕФКУМОНкЃЎвЛЬьМзЁЂввСНШЫЕНЫЩЛЈНЕФ![]() ДІЕігуЃЌЭЛШЛЗЂЯждк
ДІЕігуЃЌЭЛШЛЗЂЯждк![]() ДІгавЛШЫВЛЩїТфШыНжаКєКАОШУќЃЎШчЭМЃЌдк
ДІгавЛШЫВЛЩїТфШыНжаКєКАОШУќЃЎШчЭМЃЌдк![]() ДІВтЕУ
ДІВтЕУ![]() ДІдк
ДІдк![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЃЌНєМБЙиЭЗЃЌМзЁЂввЖўШЫзМБИТэЩЯОШШЫЃЌжЛМћМзТэЩЯДг
ЗНЯђЃЌНєМБЙиЭЗЃЌМзЁЂввЖўШЫзМБИТэЩЯОШШЫЃЌжЛМћМзТэЩЯДг![]() ДІЬјЫЎгЮЯђ
ДІЬјЫЎгЮЯђ![]() ДІОШШЫЃЛДЫЪБввДг
ДІОШШЫЃЛДЫЪБввДг![]() биАЖБпЭље§ЖЋЗНЯђБМХм40УзЕНДя
биАЖБпЭље§ЖЋЗНЯђБМХм40УзЕНДя![]() ДІЃЌдйДг
ДІЃЌдйДг![]() ДІЯТЫЎгЮЯђ
ДІЯТЫЎгЮЯђ![]() ДІОШШЫЃЌвбжЊ
ДІОШШЫЃЌвбжЊ![]() ДІдк
ДІдк![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЩЯЃЌЧвМзЁЂввЖўШЫдкЫЎжагЮНјЕФЫйЖШОљЮЊ1Уз/УыЃЌввдкАЖБпЩЯБМХмЕФЫйЖШЮЊ8Уз/УыЃЎЃЈзЂЃКЫЎЫйКіТдВЛМЦЃЉ
ЗНЯђЩЯЃЌЧвМзЁЂввЖўШЫдкЫЎжагЮНјЕФЫйЖШОљЮЊ1Уз/УыЃЌввдкАЖБпЩЯБМХмЕФЫйЖШЮЊ8Уз/УыЃЎЃЈзЂЃКЫЎЫйКіТдВЛМЦЃЉ
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉЪдЮЪМзЁЂввЖўШЫЫФмЯШОШЕНШЫЃЌЧыЭЈЙ§МЦЫуЫЕУїРэгЩЃЎЃЈ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
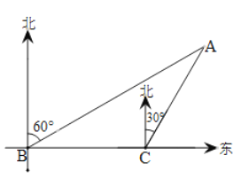
ЁОЬтФПЁПШчЭМ1ЃЌСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() Чв
Чв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
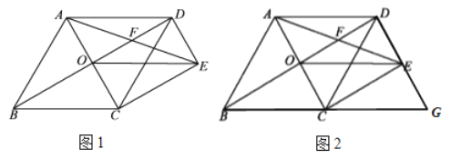
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄ![]() КЭ
КЭ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌжБНгаДГіЭМжаЫљгаЕФЦНааЫФБпаЮЃЎЃЈГ§ЫФБпаЮ
ЃЌВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌжБНгаДГіЭМжаЫљгаЕФЦНааЫФБпаЮЃЎЃЈГ§ЫФБпаЮ![]() КЭЫФБпаЮ
КЭЫФБпаЮ![]() ЭтЃЉ
ЭтЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊПЊеЙШЋПЦДѓдФЖСЛюЖЏЃЌбЇаЃЛЈЗбСЫ3400дЊдкЪщЕъЙКТђСЫ40ЬзЙХЕфЮФбЇЪщМЎКЭ20ЬзЯжДњЮФбЇЪщМЎЃЌУПЬзЯжДњЮФбЇЪщМЎБШУПЬзЙХЕфЮФбЇЪщМЎЖрЛЈ20дЊ.
ЃЈ1ЃЉЧѓУПЬзЙХЕфЮФбЇЯАЪщМЎКЭЯжДњЮФбЇЪщМЎЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЮЊТњзубЇЩњЕФдФЖСашЧѓЃЌбЇаЃМЦЛЎгУВЛГЌЙ§2500дЊдйДЮЙКТђЙХЕфЮФбЇКЭЯжДњЮФбЇЪщМЎЙВ40ЬзЃЌОЪаГЁЕїВщЕУжЊЃЌУПЬзЙХЕфЮФбЇЪщМЎМлИёЩЯИЁСЫ20%ЃЌУПЬзЯжДњЮФбЇЪщМЎМлИёЯТЕїСЫ10%ЃЌбЇаЃзюЖрФмЙКТђЖрЩйЬзЯжДњЮФбЇЪщМЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1=kx+bЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈ1ЃЌnЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈ1ЃЌnЃЉСНЕуЃЎ
ЃЈ1ЃЉЪдШЗЖЈЩЯЪіЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЎ
ЃЈ3ЃЉБШНЯy1КЭy2ЕФДѓаЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИЃжнЕчаХЙЋЫОПЊЩшСЫAЁЂBСНжжЪаФквЦЖЏЭЈаХвЕЮёЃКAжжЪЙгУепУПдТашНЩ18дЊдТзтЗбЃЌШЛКѓУПЭЈЛА1ЗжжгЃЌдйИЖЛАЗб0.1дЊЃЛBжжЪЙгУепВЛНЩдТзтЗбЃЌУПЭЈЛА1ЗжжгЃЌИЖЛАЗб0.3дЊЃЎШєвЛИідТФкЭЈЛАЪБМфЮЊxЗжжгЃЌAЁЂBСНжжЕФЗбгУЗжБ№ЮЊ![]() КЭ
КЭ![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЪдЗжБ№аДГі![]() ЁЂ
ЁЂ![]() гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉУПдТЭЈЛАЪБМфЮЊЖрГЄЪБЃЌПЊЭЈAжжвЕЮёКЭBжжвЕЮёЗбгУвЛбљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
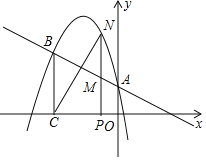
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§y=ax2Љ![]() x+cЕФЭМЯѓОЙ§ЕуAЃЈ0ЃЌ1ЃЉЃЌBЃЈЉ3ЃЌ
x+cЕФЭМЯѓОЙ§ЕуAЃЈ0ЃЌ1ЃЉЃЌBЃЈЉ3ЃЌ ![]() ЃЉЃЌAЕудкyжсЩЯЃЌЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЎ
ЃЉЃЌAЕудкyжсЩЯЃЌЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНКЭЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуNЪЧЖўДЮКЏЪ§ЭМЯѓЩЯвЛЕуЃЈЕуNдкABЩЯЗНЃЉЃЌЙ§NзїNPЁЭxжсЃЌДЙзуЮЊЕуPЃЌНЛABгкЕуMЃЌЧѓMNЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуNЪЧЖўДЮКЏЪ§ЭМЯѓЩЯвЛЕуЃЈЕуNдкABЩЯЗНЃЉЃЌЪЧЗёДцдкЕуNЃЌЪЙЕУBMгыNCЯрЛЅДЙжБЦНЗжЃПШєДцдкЃЌЧѓГіЫљгаТњзуЬѕМўЕФNЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com