
【题目】如图1,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
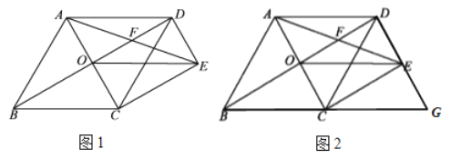
(1)求证:![]() ;
;
(2)如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形
,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形![]() 和四边形
和四边形![]() 外)
外)
科目:初中数学 来源: 题型:
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 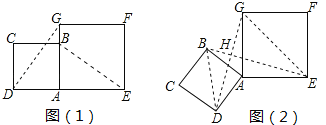
查看答案和解析>>
科目:初中数学 来源: 题型:
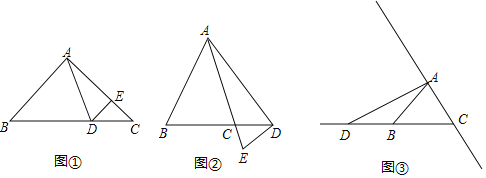
【题目】如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE= ,此时![]() = ;
= ;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系: ;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE= °(友情提醒:可利用图③画图分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上一点,C、D两点分别从P、B出发以1cm/s、2 cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置: ![]()
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求![]() 的值。
的值。
![]()
(3)在(1)的条件下,若C、D运动5秒后,恰好有![]() ,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②![]() 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
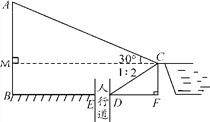
【题目】城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com