
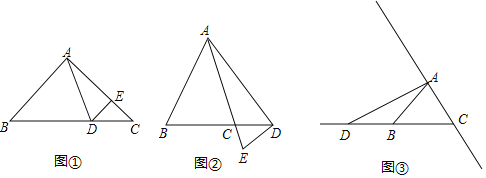
【题目】如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE= ,此时![]() = ;
= ;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系: ;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE= °(友情提醒:可利用图③画图分析)
【答案】(1)30°,2;(2)∠BAD=2∠CDE;理由见解析;(3)∠BAD=2∠CDE ;(4)∠CDE=13或77°
【解析】
(1)根据三角形内角和与三角形外角的性质可得结论;
(2)设∠DAE=x,∠BAC=y,同理可得∠BAD与∠CDE的数量关系;
(3)设∠DAE=x,∠BAC=y,同理可得∠BAD与∠CDE的数量关系;
(4)分两种情况讨论,同理可计算∠CDE的度数.
解:(1)如图,
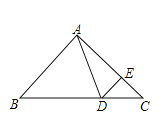
∵∠DAE=40°,∠ADE=∠AED,
∴∠ADE=70°,
∵∠BAC=100°,
∴∠BAD=∠BAC﹣∠DAE=100°﹣40°=60°,
∵∠B=∠C=40°,
∴∠ADC=∠B+∠BAD=40°+60°=100°,
∴∠CDE=30°,
∴![]() =2,
=2,
故答案为:30°,2;
(2)如图,∠BAD与∠CDE的数量关系是:∠BAD=2∠CDE;

理由是:设∠DAE=x,∠BAC=y,则∠BAD=y﹣x,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=![]() ,
,
∵∠B=∠C=![]() ,
,
∴∠ADC=∠B+∠BAD=![]() +y﹣x=90°+
+y﹣x=90°+![]() y﹣x,
y﹣x,
∴∠CDE=∠ADC﹣∠ADE=90°+![]() y﹣x﹣
y﹣x﹣![]() =
=![]() ,
,
∴∠BAD=2∠CDE;
(3)如图,∠BAD与∠CDE的数量关系:∠BAD=2∠CDE,
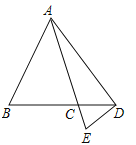
理由是:设∠DAE=x,∠BAC=y,则∠BAD=x+y,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=∠E=![]() ,
,
∵∠B=![]() ,
,
∴∠ACD=∠B+∠BAC=∠E+∠CDE,
∴![]() +y=
+y=![]() +∠CDE,
+∠CDE,
∴∠CDE=![]() (x+y),
(x+y),
∴∠BAD=2∠CDE;
故答案为:∠BAD=2∠CDE;
(4)分两种情况:
①当E在射线CA上时,如图所示,
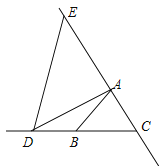
设∠DAE=x,∠BAC=y,则x+y=180°﹣26°=154°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=![]() ,
,
∵∠C=![]() ,
,
△CDE中,∠CDE=180°﹣∠AED﹣∠C=180°﹣![]() ﹣
﹣![]() =
=![]() (x+y)=
(x+y)=![]() =77°
=77°
②当E在射线AC上时,如图所示,
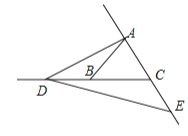
设∠DAE=x,∠BAC=y,则x﹣y=26°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=![]() ,
,
∵∠ACB=![]() ,
,
△CDE中,∠CDE=∠ACB﹣∠AED=![]() ﹣
﹣![]() =
=![]() (x﹣y)=
(x﹣y)=![]() =13°,
=13°,
综上,∠CDE=13°或77°;
故答案为:13或77.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AE⊥BD于C,AB=DE,∠A=30°,∠E=50°,F是DE的中点,则∠DBF的度数等于( )

A.10°B.20°C.30°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③ 2a+b=0;④b2-4ac>0 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有()

A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
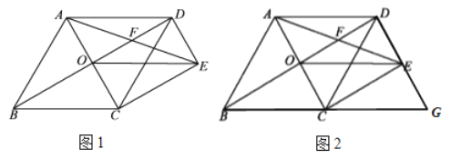
(1)求证:![]() ;
;
(2)如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形
,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形![]() 和四边形
和四边形![]() 外)
外)
查看答案和解析>>
科目:初中数学 来源: 题型:
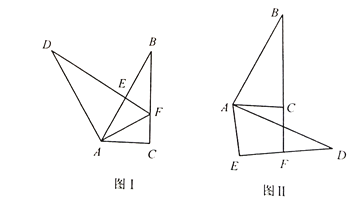
【题目】(1)如图1,在△ABC中,∠ACB=90°,点D在△ABC外,连接AD,作DE⊥AB,交BC于点F,AD=AB,AE=AC,连接AF,则DF,BC,CF间的等量关系是 ;
(2)如图2,AB=AD,AC=AE,∠ACB=∠AED=90°,延长BC交DE于点F,写出DF,BC,CF间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
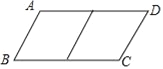
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形,例如:如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)理解与判断:
邻边长分别为1和3的平行四边形是 阶准菱形;
邻边长分别为3和4的平行四边形是 阶准菱形;
(2)操作、探究与计算:
①已知ABCD的邻边长分别为2,a(a>2),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=7b+r,b=4r,请写出ABCD是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.

(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com