
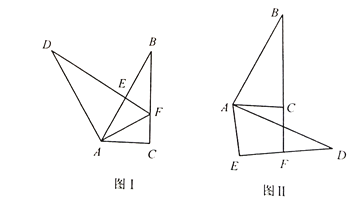
【题目】(1)如图1,在△ABC中,∠ACB=90°,点D在△ABC外,连接AD,作DE⊥AB,交BC于点F,AD=AB,AE=AC,连接AF,则DF,BC,CF间的等量关系是 ;
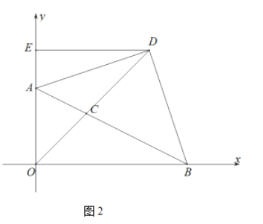
(2)如图2,AB=AD,AC=AE,∠ACB=∠AED=90°,延长BC交DE于点F,写出DF,BC,CF间的等量关系,并证明你的结论.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随机抽取某城市天的空气质量状况统计如下:
污染指数( |
|
|
|
|
|
|
天数( |
|
|
|
|
|
|
(其中![]() 时,空气质量为优;
时,空气质量为优;![]() 时,空气质量为良;
时,空气质量为良;![]() 时,空气质量为轻微污染)
时,空气质量为轻微污染)
(1)这![]() 天中,空气质量为轻微污染的天数所占的百分数是多少?
天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以![]() 天记)中有多少天空气质量到良以上?
天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
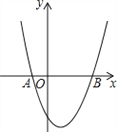
【题目】如图,已知抛物线![]() 经过A(﹣1,0)、B(3,0)两点.
经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
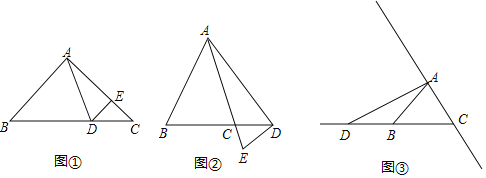
【题目】如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE= ,此时![]() = ;
= ;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系: ;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE= °(友情提醒:可利用图③画图分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
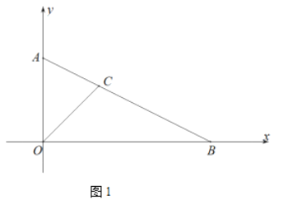
(1)如图1,求![]() 的长;
的长;
(2)如图2,![]() 是
是![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,若点
,若点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的关系;
的关系;
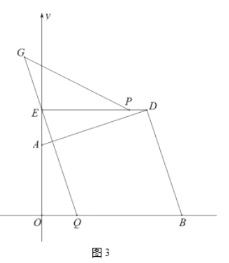
(3)在(2)的条件下,如图3,线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 值?
值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
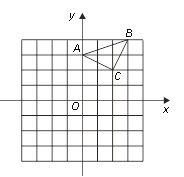
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com