
【题目】如图,已知抛物线![]() 经过A(﹣1,0)、B(3,0)两点.
经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
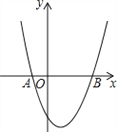
【答案】(1)抛物线的解析式为y=x2﹣2x﹣3,顶点坐标为(1,﹣4);(2)由图可得当0<x<3时,﹣4≤y<0;(3)P点坐标为(﹣2,5)或(4,5).
【解析】试题分析:(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式,再利用配方法即可求出抛物线顶点坐标;
(2)结合函数图象以及A、B点的坐标即可得出结论;
(3)设P(x,y),根据三角形的面积公式以及S△PAB=10,即可算出y的值,代入抛物线解析式即可得出点P的坐标.
试题解析:
解:(1)把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4);
(2)由图可得当0<x<3时,﹣4≤y<0;
(3)∵A(﹣1,0)、B(3,0),
∴AB=4,
设P(x,y),则S△PAB=![]() AB|y|=2|y|=10,
AB|y|=2|y|=10,
∴|y|=5,
∴y=±5;
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).


科目:初中数学 来源: 题型:
【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③ 2a+b=0;④b2-4ac>0 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有()

A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB=90°,点D在△ABC外,连接AD,作DE⊥AB,交BC于点F,AD=AB,AE=AC,连接AF,则DF,BC,CF间的等量关系是 ;
(2)如图2,AB=AD,AC=AE,∠ACB=∠AED=90°,延长BC交DE于点F,写出DF,BC,CF间的等量关系,并证明你的结论.
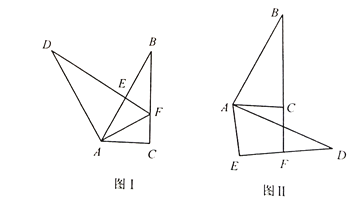
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com