
【题目】平面直角坐标系中,一次函数![]() 的图像交x轴于点A,交y轴于点B且与反比例函数
的图像交x轴于点A,交y轴于点B且与反比例函数![]() (k为常数,k≠0)的图象分别交于C、D两点,过点C作
(k为常数,k≠0)的图象分别交于C、D两点,过点C作![]() 轴于M,
轴于M,![]() ,
,![]() ,
,![]()
(1)求直线AB和反比例函数的解析式.
(2)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
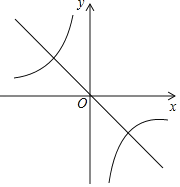
【题目】反比函数![]() 的图象如图所示.
的图象如图所示.
(1)求m的值;
(2)当x>﹣1时,y的取值范围是 ;
(3)当直线y2=﹣x与双曲线![]() 交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是
是![]() 轴上的一个动点,设点
轴上的一个动点,设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
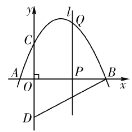
(1)求点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将抛物线y=ax2(﹣1<a<0)平移到顶点恰好落在直线y=x﹣3上,并设此时抛物线顶点的横坐标为m.
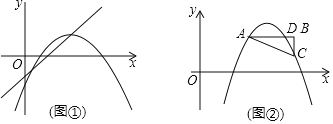
(1)求抛物线的解析式(用含a、m的代数式表示)
(2)如图②,Rt△ABC与抛物线交于A、D、C三点,∠B=90°,AB∥x轴,AD=2,BD:BC=1:2.
①求△ADC的面积(用含a的代数式表示)
②若△ADC的面积为1,当2m﹣1≤x≤2m+1时,y的最大值为﹣3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了如下框中的题目:

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=”).
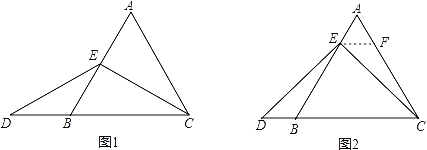
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(a﹣1)x2+3ax+1图象上的四个点的坐标为(x1,m),(x2,m),(x3,n),(x4,n),其中m<n.下列结论可能正确的是( )
A.若a>![]() ,则 x1<x2<x3<x4
,则 x1<x2<x3<x4
B.若a>![]() ,则 x4<x1<x2<x3
,则 x4<x1<x2<x3
C.若a<﹣![]() ,则 x1<x3<x2<x4
,则 x1<x3<x2<x4
D.若a<﹣![]() ,则 x3<x2<x1<x4
,则 x3<x2<x1<x4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个斜边长是8的Rt△AEC,一个斜边长是6的Rt△AFB,一个正方形AEDF,拼成一个如图所示的Rt△BCD,则Rt△AEC和Rt△AFB的面积之和是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
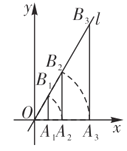
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交过原点与
轴的垂线交过原点与![]() 轴夹角为
轴夹角为![]() 的直线
的直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ……按此做法进行下去,则点
……按此做法进行下去,则点![]() 的坐标是_____.
的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为助力我省脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年六月底收购一批农产品,七月份销售![]() 袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到
袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到![]() 袋.
袋.
(1)求八、九这两个月销售量的月平均增长率;
(2)该网店十月降价促销,经调查发现,若该农产品每袋降价![]() 元,销售量可增加
元,销售量可增加![]() 袋,当农产品每袋降价多少元时,这种农产品在十月份可获利
袋,当农产品每袋降价多少元时,这种农产品在十月份可获利![]() 元?(若农产品每袋进价
元?(若农产品每袋进价![]() 元,原售价为每袋
元,原售价为每袋![]() 元)
元)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com