
【题目】一个斜边长是8的Rt△AEC,一个斜边长是6的Rt△AFB,一个正方形AEDF,拼成一个如图所示的Rt△BCD,则Rt△AEC和Rt△AFB的面积之和是_____.

科目:初中数学 来源: 题型:
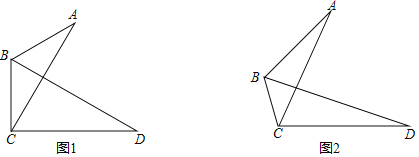
【题目】在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.
(1)如图1,若AB=BC,求证:BD平分∠ABC;
(2)如图2,若AB=2BC,
①求![]() 的值;
的值;
②连接AD,当S△ABC=![]() 时,直接写出四边形ABCD的面积为 .
时,直接写出四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(点P在△ABC内部),连接AP、BP、BQ.

(1)求证:AP=BQ;
(2)当PQ⊥BQ时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,一次函数![]() 的图像交x轴于点A,交y轴于点B且与反比例函数
的图像交x轴于点A,交y轴于点B且与反比例函数![]() (k为常数,k≠0)的图象分别交于C、D两点,过点C作
(k为常数,k≠0)的图象分别交于C、D两点,过点C作![]() 轴于M,
轴于M,![]() ,
,![]() ,
,![]()
(1)求直线AB和反比例函数的解析式.
(2)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全力抗击新型冠状病毒感染肺炎,减少相互感染,每个人出门都必须带上口罩,所以KN95型的口罩需求量越来越大.某大型口罩工厂接到生产200万副KN95型口罩的生产任务,计划在若干天完成,由于情况疫情紧急,工厂全体不畏艰苦,工人全力以赴,每天比原计划多生产5万副口罩,结果只用了原计划时间的![]() 就圆满完成生产任务,则原计划每天生产_________万副口罩.
就圆满完成生产任务,则原计划每天生产_________万副口罩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B![]() ,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
(1)若![]() ,在点C(0,
,在点C(0,![]() ),D
),D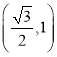 ,E
,E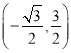 中,线段AB的“等角点”是 ;
中,线段AB的“等角点”是 ;
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(6,0),∠OMN=30°.
①线段AB的“等角点”P在直线MN上,且∠ABP=90°,求点P的坐标;
②在①的条件下,过点B作BQ⊥PA,交MN于点Q,求∠AQB的度数;
③若线段AB的所有“等角点”都在△MON内部,则t的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
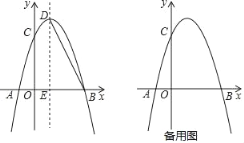
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBFG,随着点P的运动,正方形的大小、位置也随着改变,当顶点F或G恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com