
【题目】如图①,将抛物线y=ax2(﹣1<a<0)平移到顶点恰好落在直线y=x﹣3上,并设此时抛物线顶点的横坐标为m.
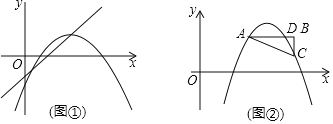
(1)求抛物线的解析式(用含a、m的代数式表示)
(2)如图②,Rt△ABC与抛物线交于A、D、C三点,∠B=90°,AB∥x轴,AD=2,BD:BC=1:2.
①求△ADC的面积(用含a的代数式表示)
②若△ADC的面积为1,当2m﹣1≤x≤2m+1时,y的最大值为﹣3,求m的值.
【答案】(1)y=ax2﹣2amx+am2+m﹣3;(2)①﹣![]() ;②0或
;②0或![]()
【解析】
(1)抛物线的顶点在直线y=x﹣3上,横坐标为m,则顶点的坐标为(m,m﹣3),即可求解;
(2)①求出点C坐标(m+1+t,a+m﹣3﹣2t),利用点C在抛物线上,则:a+m﹣3﹣2t=a(m+t+1﹣m)2+m﹣3,求得:t=﹣![]() ,利用S△ADC=
,利用S△ADC=![]() ADCB即可求解;②分m>2m+1、2m﹣1≤m≤2m+1、m<2m+1三种情况,求解即可.
ADCB即可求解;②分m>2m+1、2m﹣1≤m≤2m+1、m<2m+1三种情况,求解即可.
解:(1)抛物线的顶点在直线y=x﹣3上,横坐标为m,
则顶点的坐标为(m,m﹣3),
则抛物线的表达式为:y=a(x﹣m)2+m﹣3=ax2﹣2amx+am2+m﹣3;
(2)①如图所示,AB∥x轴,AD=2,
∴点D(m+1,a+m﹣3),
设:BD=t,
∵BD:BC=1:2,则BC=2t,
则点C(m+1+t,a+m﹣3﹣2t),
又点C在抛物线上,
则:a+m﹣3﹣2t=a(m+t+1﹣m)2+m﹣3,
解得:t=0(舍去)或﹣![]() ,
,
∴S△ADC=![]() ADCB=﹣
ADCB=﹣![]() ;
;
②若△ADC的面积为1,则=﹣![]() =1,
=1,
解得:a=﹣![]() ;
;
∴抛物线的表达式为:y=﹣![]() (x﹣m)2+m﹣3;
(x﹣m)2+m﹣3;
当m>2m+1时,即:m<﹣1时,
﹣![]() (2m+1﹣m)2+m﹣3=﹣3,
(2m+1﹣m)2+m﹣3=﹣3,
整理得:4m2+3m+4=0,
△=b
当2m﹣1≤m≤2m+1时,即:﹣1≤m≤1,
则m﹣3=﹣3,解得:m=0;
当m<2m﹣1时,即:m>1,
﹣![]() (2m﹣1﹣m)2+m﹣3=﹣3,
(2m﹣1﹣m)2+m﹣3=﹣3,
整理并解得:m=![]() (舍去负值),
(舍去负值),
故:m的值为:0或![]() .
.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
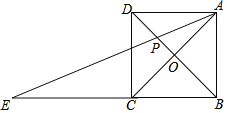
(1)求∠DAE的度数;
(2)求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD边长为6,点E,F分别是AB,CD的中点,点G,H分别在AD,AB上,将纸片沿直线GH对折,当顶点A与线段EF的三等分点重合时,AH的长为_____.
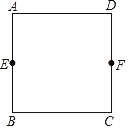
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;
(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(点P在△ABC内部),连接AP、BP、BQ.

(1)求证:AP=BQ;
(2)当PQ⊥BQ时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=![]() 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).

(1)发现C船时,A、B、C三船所在位置的坐标分别为A(_______,_______)、B(_______,_______)和C(_______,_______);
(2)发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,一次函数![]() 的图像交x轴于点A,交y轴于点B且与反比例函数
的图像交x轴于点A,交y轴于点B且与反比例函数![]() (k为常数,k≠0)的图象分别交于C、D两点,过点C作
(k为常数,k≠0)的图象分别交于C、D两点,过点C作![]() 轴于M,
轴于M,![]() ,
,![]() ,
,![]()
(1)求直线AB和反比例函数的解析式.
(2)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com