
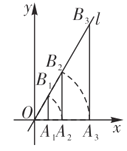
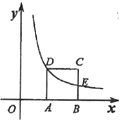
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交过原点与
轴的垂线交过原点与![]() 轴夹角为
轴夹角为![]() 的直线
的直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ……按此做法进行下去,则点
……按此做法进行下去,则点![]() 的坐标是_____.
的坐标是_____.
【答案】![]()
【解析】
先根据一次函数方程式求出B1点的坐标,再根据B1点的坐标求出A2点的坐标,得出B2的坐标,以此类推总结规律便可求出点B2019的坐标.
∵过点A1作x轴的垂线交过原点与x轴夹角为![]() 的直线l于点B1,OA1=2,
的直线l于点B1,OA1=2,
∴∠B1OA1=60![]() ,∴∠OB1A1=30
,∴∠OB1A1=30![]()
∴OB1= OA1=4,B1A1=![]()
∴B1(2,![]() )
)
∴直线y=![]() x,
x,
以原O为圆心,OB1长为半径画弧x轴于点A2,则OA2=OB1,
∵OA2=4,
∴点A2的坐标为(4,0),
∴B2的坐标为(4,4![]() ),即(22,22×
),即(22,22×![]() ),
),
OA3=![]()
∴点A3的坐标为(8,0),B3(8,8![]() ),
),
……,
以此类推便可得出点A2019的坐标为(22019,0),点B2019的坐标为![]() ;
;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD边长为6,点E,F分别是AB,CD的中点,点G,H分别在AD,AB上,将纸片沿直线GH对折,当顶点A与线段EF的三等分点重合时,AH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,一次函数![]() 的图像交x轴于点A,交y轴于点B且与反比例函数
的图像交x轴于点A,交y轴于点B且与反比例函数![]() (k为常数,k≠0)的图象分别交于C、D两点,过点C作
(k为常数,k≠0)的图象分别交于C、D两点,过点C作![]() 轴于M,
轴于M,![]() ,
,![]() ,
,![]()
(1)求直线AB和反比例函数的解析式.
(2)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B![]() ,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
(1)若![]() ,在点C(0,
,在点C(0,![]() ),D
),D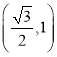 ,E
,E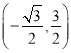 中,线段AB的“等角点”是 ;
中,线段AB的“等角点”是 ;
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(6,0),∠OMN=30°.
①线段AB的“等角点”P在直线MN上,且∠ABP=90°,求点P的坐标;
②在①的条件下,过点B作BQ⊥PA,交MN于点Q,求∠AQB的度数;
③若线段AB的所有“等角点”都在△MON内部,则t的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学校的体育活动,某学校计划购进甲、乙两种篮球,根据市场调研发现,如果购进甲篮球2个和乙篮球3个共需270元;购进甲篮球3个和乙篮球2个共需230元.
(1)求甲、乙两种篮球每个的售价分别是多少元?
(2)为满足开展体育活动的需求,学校计划购进甲、乙两种篮球共100个,由于购货量大,和商场协商,商场决定甲篮球以九折出售,乙篮球以八折出售,学校要求甲种篮球的数量不少于乙种篮球数量的4倍,甲种篮球的数量不多于90个,请你求出学校花最少钱的进货方案;
(3)学校又拿出省下的290元购买跳绳和毽子两种体育器材,跳绳10元一根,毽子5元一个,在把钱用尽的情况下,有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴上,反比例函数
轴正半轴上,反比例函数![]() 的图像在第一象限的图像经过点
的图像在第一象限的图像经过点![]() ,交
,交![]() 于
于![]() .
.
(1)当点![]() 的坐标为
的坐标为![]() 时,求
时,求![]() 和
和![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com