
【题目】受非洲猪瘟的影响,2019年的猪肉价格创历史新高,同时其他肉类的价格也有一定程度的上涨,某超市11月份的猪肉销量是羊肉销量的![]() 倍,且猪肉价格为每千克
倍,且猪肉价格为每千克![]() 元羊肉价格为每千克
元羊肉价格为每千克![]() 元.
元.
(1)若该超市11月份猪肉、羊肉的总销售额不低于![]() 万元,则11月份的猪肉销量至少多少千克?
万元,则11月份的猪肉销量至少多少千克?
(2)12月份香肠腊肉等传统美食的制作,使得市场的猪肉需求加大,12月份猪肉的销量比11月份增长了![]() ,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了
,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了![]() ,羊肉的销量是11月份猪肉销量的
,羊肉的销量是11月份猪肉销量的![]() ,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了
,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了![]() ,求
,求![]() 的值.
的值.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
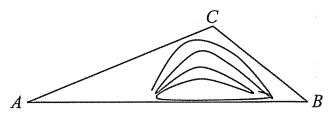
【题目】修建隧道可以方便出行.如图:![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要爬坡到山顶
地需要爬坡到山顶![]() 地,再下坡到
地,再下坡到![]() 地.若打通穿山隧道,建成直达
地.若打通穿山隧道,建成直达![]() ,
,![]() 两地的公路,可以缩短从
两地的公路,可以缩短从![]() 地到
地到![]() 地的路程.已知:从
地的路程.已知:从![]() 到
到![]() 坡面的坡度
坡面的坡度![]() ,从
,从![]() 到
到![]() 坡面的坡角
坡面的坡角![]() ,
,![]() 公里.
公里.
(1)求隧道打通后从![]() 到
到![]() 的总路程是多少公里?(结果保留根号)
的总路程是多少公里?(结果保留根号)
(2)求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程约缩短多少公里?(结果精确到0.01)(
地的路程约缩短多少公里?(结果精确到0.01)(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图1.在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() .则
.则![]() 面积的最大值是_______.
面积的最大值是_______.
(2)如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的外接圆,若
的外接圆,若![]() ,试判断
,试判断![]() 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
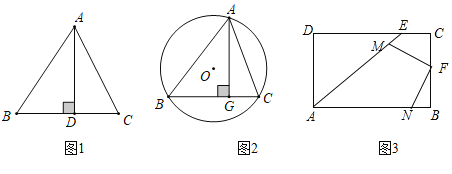
问题解决:
如图3,王老先生有一块矩形地![]() ,
,![]() ,
,![]() ,现在他想利用这块地建一个四边形鱼塘
,现在他想利用这块地建一个四边形鱼塘![]() ,且满足点
,且满足点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,这个四边形
,这个四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段路的“拥堵延时指数”计算公式为:拥堵延时指数=![]() ,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的
,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的![]() 倍,且A路段比B路段长1千米.
倍,且A路段比B路段长1千米.
(1)分别求平峰时A、B两路段的通行时间;
(2)第二季度大数据显示:在高峰时,A路段的拥堵延时指数为2,每分钟有150辆汽车进入该路段;B路段的拥堵延时指数为1.8,每分钟有125辆汽车进入该路段。第三季度,交管部门采用了智能红绿灯和潮汐车道的方式整治,拥堵状况有明显改善,在高峰时,A路段拥堵延时指数下降了a%,每分钟进入该路段的车辆增加了![]() ;B路段拥堵延时指数下降
;B路段拥堵延时指数下降![]() ,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多
,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多![]() 小时,求a的值.
小时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学一次趣味运动会50米托盘乒乓球接力项目中(即乒乓球放入托盘内,参赛队员用手托住托盘运送乒乓球),初一(1)班和初一(2)班同台竞技,某时刻,1班的小敏和2班的小文分别位于50米赛道的起点![]() 地和终点
地和终点![]() 地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在
地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在![]() 地(
地(![]() 、
、![]() 、
、![]() 在同一直线上且乒乓球落在
在同一直线上且乒乓球落在![]() 地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往
地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往![]() 地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离
地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离![]() (米)与小敏出发的时间
(米)与小敏出发的时间![]() (秒)之间的函数图象,则当小敏到达
(秒)之间的函数图象,则当小敏到达![]() 地时,小文离
地时,小文离![]() 地还有________米.
地还有________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
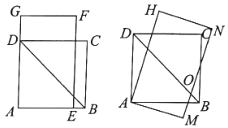
【题目】如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,长方形
的正方形,长方形![]() 的宽
的宽![]() ,长
,长![]() .将长方形
.将长方形![]() 绕点
绕点![]() 顺时针旋转15°得到长方形
顺时针旋转15°得到长方形![]() (如图所示),这时
(如图所示),这时![]() 与
与![]() 相交于点
相交于点![]() .则在图中,
.则在图中,![]() ,
,![]() 两点间的距离是( )
两点间的距离是( )
A.![]() B.5C.
B.5C.![]() D.7
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
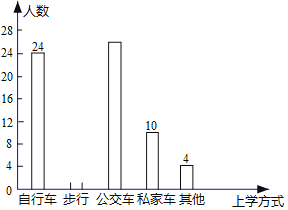
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com