
【题目】一段路的“拥堵延时指数”计算公式为:拥堵延时指数=![]() ,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的
,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的![]() 倍,且A路段比B路段长1千米.
倍,且A路段比B路段长1千米.
(1)分别求平峰时A、B两路段的通行时间;
(2)第二季度大数据显示:在高峰时,A路段的拥堵延时指数为2,每分钟有150辆汽车进入该路段;B路段的拥堵延时指数为1.8,每分钟有125辆汽车进入该路段。第三季度,交管部门采用了智能红绿灯和潮汐车道的方式整治,拥堵状况有明显改善,在高峰时,A路段拥堵延时指数下降了a%,每分钟进入该路段的车辆增加了![]() ;B路段拥堵延时指数下降
;B路段拥堵延时指数下降![]() ,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多
,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多![]() 小时,求a的值.
小时,求a的值.
【答案】(1)平峰时A路段的通行时间是![]() 小时,平峰时B路段的通行时间是
小时,平峰时B路段的通行时间是![]() 小时;(2)
小时;(2)![]() 的值是15.
的值是15.
【解析】
(1)根据题意,设平峰时B路段通行时间为![]() 小时,则平峰时A路段通行时间是
小时,则平峰时A路段通行时间是![]() ,列出方程,解方程即可得到答案;
,列出方程,解方程即可得到答案;
(2)根据题意,先求出整治前A、B路段的时间总和,然后利用含a的代数式求出整治后A、B路段的时间总和,再列出方程,求出a的值.
解:(1)设平峰时B路段通行时间为![]() 小时,则平峰时A路段通行时间是
小时,则平峰时A路段通行时间是![]() ,则
,则
![]() ,
,
解得:![]() ,
,
∴![]() (小时);
(小时);
∴平峰时A路段的通行时间是![]() 小时,平峰时B路段的通行时间是
小时,平峰时B路段的通行时间是![]() 小时;
小时;
(2)根据题意,整治前有:
高峰时,通过A路段的总时间为:![]() (分钟),
(分钟),
高峰时,通过B路段的总时间为:![]() (分钟);
(分钟);
整治前的时间总和为:![]() (分钟);
(分钟);
整治后有:通过A路段的总时间为:
![]() ;
;
通过B路段的总时间为:![]() ;
;
∴整治后的时间总和为:
![]()
![]() ;
;
∴![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
∴![]() 的值是15.
的值是15.


科目:初中数学 来源: 题型:
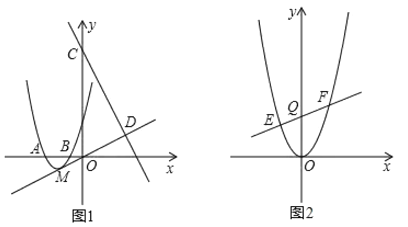
【题目】如图(1),抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图(2),将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体育考试时间越来越近,某校想了解初三年级1500名学生跳绳情况,从中随机抽查了20名男生和20名女生的跳绳成绩,收集到了以下数据:
男生:192、166,189,186,184,182,178,177,174,170,188,168,205,165,158,150,188,172,180,188
女生:186,198,162,192,188,186,185,184,180,180,186,193,178,175,172,166,155,183,187,184.
根据统计数据制作了如下统计表:
个数x | 150≤x<170 | 170≤x<185 | 185≤x<190 | x≥190 |
男生 | 5 | 8 | 5 | 2 |
女生 | 3 | 8 | a | 3 |
两组数据的极差、平均数、中位数、众数如表所示:
极差 | 平均数 | 中位数 | 众数 | |
男生 | 55 | 178 | b | c |
女生 | 43 | 181 | 184 | 186 |
(1)请将上面两个表格补充完整:a=____,b=_____,c=_____;
(2)请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分(185个及以上)的同学大约能有多少人?
(3)体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好,请你结合统计数据,写出支持江老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮看到路边上有人设摊玩“有奖掷币”游戏,规则是交2元钱可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币都正面朝上,奖金5元;如果是其他情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).
(1)小亮应不应该玩?
(2)如果有100人,每人玩一次这种游戏,设摊者约获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
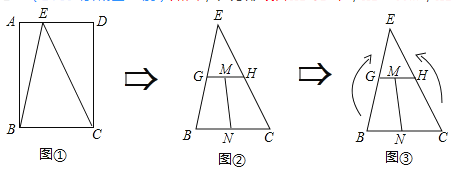
【题目】如图,矩形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图:
第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);
第二步:如图②,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;
第三步:如图③,将MN左侧纸片绕G点按顺时针旋转180,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片(裁剪和拼图过程均无缝且不重叠)则拼成的这个四边形纸片的周长的最大值为___cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=![]() 的图象相交于A(m,3
的图象相交于A(m,3![]() ),C两点,已知点B(2
),C两点,已知点B(2![]() ,2
,2![]() ),则k的值为( )
),则k的值为( )

A. 6B. ﹣6C. 6![]() D. ﹣6
D. ﹣6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟的影响,2019年的猪肉价格创历史新高,同时其他肉类的价格也有一定程度的上涨,某超市11月份的猪肉销量是羊肉销量的![]() 倍,且猪肉价格为每千克
倍,且猪肉价格为每千克![]() 元羊肉价格为每千克
元羊肉价格为每千克![]() 元.
元.
(1)若该超市11月份猪肉、羊肉的总销售额不低于![]() 万元,则11月份的猪肉销量至少多少千克?
万元,则11月份的猪肉销量至少多少千克?
(2)12月份香肠腊肉等传统美食的制作,使得市场的猪肉需求加大,12月份猪肉的销量比11月份增长了![]() ,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了
,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了![]() ,羊肉的销量是11月份猪肉销量的
,羊肉的销量是11月份猪肉销量的![]() ,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了
,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=ax2+bx+c(a>0)的图象与x轴交于A(﹣1,0),B(n,0)两点,一次函数y2=2x+b的图象过点A.
(1)若a=![]() .
.
①若二次函数y1=ax2+bx+c(a>0)与y轴交于点C,求△ABC的面积;
②设y3=y1﹣my2,是否存在正整数m,当x≥0时,y3随x的增大而增大?若存在,求出正整数m的值;若不存在,请说明理由.
(2)若![]() <a<
<a<![]() ,求证:﹣5<n<﹣4.
,求证:﹣5<n<﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
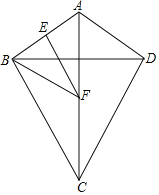
【题目】如图,在四边形ABCD中,对角线AC垂直平分BD,∠BAD=120°,AB=4,点E是AB的中点,点F是AC上一动点,则EF+BF的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com