
����Ŀ����֪���κ���y1=ax2+bx+c��a��0����ͼ����x�ύ��A����1��0����B��n��0�����㣬һ�κ���y2=2x+b��ͼ�����A��
��1����a=![]() ��
��
�������κ���y1=ax2+bx+c��a��0����y�ύ�ڵ�C�����ABC�������
����y3=y1��my2���Ƿ����������m����x��0ʱ��y3��x����������������ڣ����������m��ֵ���������ڣ���˵�����ɣ�
��2����![]() ��a��
��a��![]() ����֤����5��n����4��
����֤����5��n����4��
���𰸡���1����![]() ���ڴ��ڣ�m=1����2��������
���ڴ��ڣ�m=1����2��������
��������
��1��������A����������ʽ����b=2��c=2��a�������������߽���ʽ�������C����B���꣬�������ε������ʽ����⣻
����y3=![]() x2+2x+
x2+2x+![]() ��m��2x+2��=
��m��2x+2��=![]() x2+��2��2m��x+��
x2+��2��2m��x+��![]() ��2m�����ɶ��κ��������ʿ���m��1��������⣻
��2m�����ɶ��κ��������ʿ���m��1��������⣻
��2��y1=ax2+2x+��2��a���ĶԳ���Ϊx=��![]() =��
=��![]() ����
����![]() ��a��
��a��![]() ���ɵé�3����
���ɵé�3����![]() ����
����![]() ����A����1��0����B��n��0��������ڶԳ���Գƣ���|��1������
����A����1��0����B��n��0��������ڶԳ���Գƣ���|��1������![]() ��|=|��
��|=|��![]() ��n|��������⣮
��n|��������⣮
�⣺��1���١�y1=ax2+bx+c��a��0������A��
��a��b+c=0��
��y2=2x+b��ͼ�����A��
��b=2��
��c=2��a��
��a=![]() ��
��
��c=2��![]() ��
��
��y1=![]() x2+2x+
x2+2x+![]() ��
��
�������y1=![]() x2+2x+
x2+2x+![]() ��y�ύ�ڵ�C����x�ύ��A����1��0����B��n��0�����㣬
��y�ύ�ڵ�C����x�ύ��A����1��0����B��n��0�����㣬
����C��0��![]() ������B����3��0����
������B����3��0����
��AB=2��
���ABC�����=![]() ��2��
��2��![]() ��
��
��y3=![]() x2+2x+
x2+2x+![]() ��m��2x+2��=
��m��2x+2��=![]() x2+��2��2m��x+��
x2+��2��2m��x+��![]() ��2m����
��2m����
����x��0ʱ��y3��x�����������
���Գ���x=��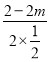 =2m��2��0��
=2m��2��0��
��m��1��
��m����������
��m=1��
��2����y1=ax2+2x+��2��a���ĶԳ���Ϊx=��![]() =��
=��![]() ��
��
����![]() ��a��
��a��![]() ��
��
����3����![]() ����
����![]() ��
��
����A����1��0����B��n��0��������ڶԳ���Գƣ�
��|��1������![]() ��|=|��
��|=|��![]() ��n|��
��n|��
��n=��![]() +1��n=��1����ȥ����
+1��n=��1����ȥ����
����5��n����4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ������������
������������![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬����
�㣬����![]() ��
��![]() .
.

��1����ֱ��![]() ����
����![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
��2���������ߵĶԳ���![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �ľ����뵽��
�ľ����뵽��![]() �ľ���֮����С�������
�ľ���֮����С�������![]() �����ꣻ
�����ꣻ
��3�����![]() Ϊ�����ߵĶԳ���
Ϊ�����ߵĶԳ���![]() �ϵ�һ�����㣬��ʹ
�ϵ�һ�����㣬��ʹ![]() Ϊֱ�������εĵ�
Ϊֱ�������εĵ�![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��·����ӵ����ʱָ�������㹫ʽΪ��ӵ����ʱָ��=![]() ��ָ��Խ��·Խ�¡��ߵ´�������ʾ�ڶ���������ӵ����ʱָ���״���ȫ�����ס�Ϊ�ˣ����ܲ�����A��B��ӵ��·�ν��е��У�A·��ƽ��ʱ����ͨ��ƽ��ʱ��Ϊ45ǧ��/ʱ��B·��ƽ��ʱ����ͨ��ƽ��ʱ��Ϊ50ǧ��/ʱ��ƽ��ʱA·��ͨ��ʱ����B·��ͨ��ʱ���
��ָ��Խ��·Խ�¡��ߵ´�������ʾ�ڶ���������ӵ����ʱָ���״���ȫ�����ס�Ϊ�ˣ����ܲ�����A��B��ӵ��·�ν��е��У�A·��ƽ��ʱ����ͨ��ƽ��ʱ��Ϊ45ǧ��/ʱ��B·��ƽ��ʱ����ͨ��ƽ��ʱ��Ϊ50ǧ��/ʱ��ƽ��ʱA·��ͨ��ʱ����B·��ͨ��ʱ���![]() ������A·�α�B·�γ�1ǧ�ף�
������A·�α�B·�γ�1ǧ�ף�
��1���ֱ���ƽ��ʱA��B��·�ε�ͨ��ʱ�䣻
��2���ڶ����ȴ�������ʾ���ڸ߷�ʱ��A·�ε�ӵ����ʱָ��Ϊ2��ÿ������150�����������·�Σ�B·�ε�ӵ����ʱָ��Ϊ1.8��ÿ������125�����������·�Ρ��������ȣ����ܲ��Ų��������ܺ��̵ƺͳ�ϫ�����ķ�ʽ���Σ�ӵ��״�������Ը��ƣ��ڸ߷�ʱ��A·��ӵ����ʱָ���½���a%��ÿ���ӽ����·�εij���������![]() ��B·��ӵ����ʱָ���½�
��B·��ӵ����ʱָ���½�![]() ��ÿ���ӽ����·�εij���������a�������������κ�ÿ���ӷֱ������·�εij���ͨ������·������ʱ���ܺͣ�������ǰÿ���ӷֱ����������·�ij���ͨ������·������ʱ���ܺͶ�
��ÿ���ӽ����·�εij���������a�������������κ�ÿ���ӷֱ������·�εij���ͨ������·������ʱ���ܺͣ�������ǰÿ���ӷֱ����������·�ij���ͨ������·������ʱ���ܺͶ�![]() Сʱ����a��ֵ��
Сʱ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �������Σ�������
�������Σ�������![]() �Ŀ�
�Ŀ�![]() ����
����![]() ����������
����������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת15��õ�������
˳ʱ����ת15��õ�������![]() ����ͼ��ʾ������ʱ
����ͼ��ʾ������ʱ![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������ͼ�У�
������ͼ�У�![]() ��
��![]() �����ľ����ǣ� ��
�����ľ����ǣ� ��
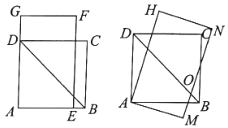
A.![]() B.5C.
B.5C.![]() D.7
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(��3��y1)��B(2��y2)����������y��ax2+bx+c�ϣ���P(m��n)�Ǹ������ߵĶ��㣬��y1��y2��n����m��ȡֵ��Χ��(����)
A.��3��m��2B.��![]() ��m��-
��m��-![]() C.m����
C.m����![]() D.m��2
D.m��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��F���ı���ABCD�ĶԽ����ӳ����ϣ�AE=CF��DE��BF����1=��2��
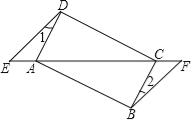
��1����֤����AED�ա�CFB��
��2����AD��CD���ı���ABCD��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������һ��ɱ�Ϊ20Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
���۵��� | �� | 30 | 40 | 50 | 60 | �� |
ÿ�������� | �� | 500 | 400 | 300 | 200 | �� |
��1���о����֣�ÿ��������![]() �뵥��
�뵥��![]() ����һ�κ�����ϵ�����
����һ�κ�����ϵ�����![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���45Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����²��ϣ��������Ӧ����
쳲�������Լ1170-1250�����������ѧ�ң�1202�꣬д�ˡ������顷һ�飬���ǵ�һ���о���ӡ�ȺͰ�������ѧ���۵�ŷ���ˣ��������ڰ����������ǡ�ϣ�����Լ������������ͷ���������˹�ȵ��о���ѧ�����о���һ�зdz����������0��1��1��2��3��5��8��13��21��34��55��89��144����������������Ϊ쳲��������У����ص��Ǵӵ�3�ʼ��ÿһ�����ǰ����֮�ͣ�쳲��������л��кܶ���Ȥ�����ʣ���ʵ��������Ҳ�й㷺��Ӧ�ã�

����1����д�±���д��ͨ������㷢�ֵĹ��ɣ�
�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | ��7�� | ��8�� | ��9�� | �� |
��һ���ƽ�� | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | �� |
��һ���ǰ��������Ļ� | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | �� |
���ɣ�_____________��
��2�����г�Ϊ![]() ����˿��Ҫ�س�
����˿��Ҫ�س�![]() С�Σ�ÿ�εij��Ȳ�С��
С�Σ�ÿ�εij��Ȳ�С��![]() ���������������С�ζ�����ƴ�������Σ���
���������������С�ζ�����ƴ�������Σ���![]() �����ֵΪ___________________��
�����ֵΪ___________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������⣺����![]() =-a����a��0������a>
=-a����a��0������a>![]() ����a2>b2��������λ��ͼ��һ��������ͼ�Σ���ƽ���ı��ε�����Ա߷ֱ���ȣ�����ԭ�������������Ϊ������ĸ�����( )
����a2>b2��������λ��ͼ��һ��������ͼ�Σ���ƽ���ı��ε�����Ա߷ֱ���ȣ�����ԭ�������������Ϊ������ĸ�����( )
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com