
【题目】完成题目:
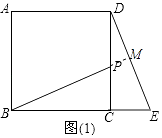
(1)如图(1),点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:BP=DE且BP⊥DE;
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点.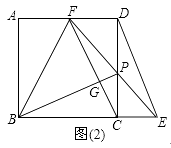
①若BC=2CE时,求证:BP⊥CF;
②若BC=nCE(n是大于1的实数)时,记△BPF的面积为S1 , △DPE的面积为S2 . 求证:S1=(n+1)S2 .
【答案】
(1)证明:延长BP交DE于M,
在△BCP和△DCE中,
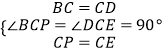 ,
,
∴△BCP≌△DCE,
∴BP=DE,∠CBP=∠CDE,
∵∠CDE+∠E=90°,
∴∠CBP+∠E=90°,即BP⊥DE
(2)证明:①∵CP=CE,∠PCE=90°,
∴∠CPE=45°,
∴∠FPD=∠CPE=45°,
∴∠PFD=45°,
∴FD=PD,
∵BC=2CE,
∴CD=2CE=2PC,即DP=CP,
∴DF=CP,
在△BCP和△CDF中,
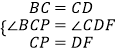 ,
,
∴△BCP≌△CDF,
∴∠FCD=∠CBP,
∵∠CBP+∠BPC=90°,
∴∠FCD+∠BPC=90°,即BP⊥CF;
②设CE=CP=1,则BC=CD=n,DP=CD﹣CP=n﹣1,
∴FD=DP=n﹣1,
S1=S梯形BCDF﹣S△BCP﹣S△FDP
= ![]() ×(BC+DF)×CD﹣
×(BC+DF)×CD﹣ ![]() BC×CP﹣
BC×CP﹣ ![]() DF×FP
DF×FP
= ![]() (n+n﹣1)×n﹣
(n+n﹣1)×n﹣ ![]() n×1﹣
n×1﹣ ![]() (n﹣1)2
(n﹣1)2
= ![]() (n2﹣1)
(n2﹣1)
= ![]() (n+1)(n﹣1),
(n+1)(n﹣1),
S2= ![]() DP×CE=
DP×CE= ![]() (n﹣1)×1=
(n﹣1)×1= ![]() (n﹣1),
(n﹣1),
∴S1=(n+1)S2.
【解析】(1)延长BP交DE于M,证明△BCP≌△DCE,根据全等三角形的性质证明即可;(2)①根据等腰直角三角形的性质、正方形的性质证明△BCP≌△CDF,根据全等三角形的性质证明即可;②设CE=CP=1,根据题意用n表示出BC、DP,根据梯形、三角形的面积公式计算即可.


科目:初中数学 来源: 题型:
【题目】(本题满分10分)
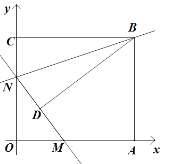
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+=0(OB>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,连接BN.将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=.
⑴ 求点B的坐标.
⑵ 求直线BN的解析式.
⑶ 将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有________人进公园,买40张门反而合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一次函数图象y=2x向右平移1个单位,所得图象对应的函数关系式为( )
A. y=2x﹣2 B. y=2x﹣1 C. y=2x+1 D. y=2x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建食堂正式投入使用,为提高服务质量,食堂管理人员对学生进行了“最受欢迎菜品”的调查统计,以下是打乱了的调查统计顺序,请按正确顺序重新排序 (只填番号)_________________.
①.绘制扇形图;②.收集最受学生欢迎菜品的数据;③.利用扇形图分析出受欢迎的统计图;④.整理所收集的数据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com