
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中 .
.
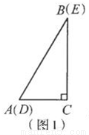
(1)操作发现(4分)
如图2,固定△ABC ,使△DEC绕点C旋转。当点D恰好落在AB边上时,填空:
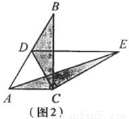
线段DE与AC的位置关系是 ;
设△BDC的面积为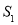 ,△AEC的面积为
,△AEC的面积为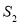 。则
。则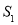 与
与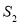 的数量关系是 。
的数量关系是 。
(2)猜想论证(4分)
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中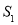 与
与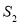 的数量关系仍然成立,并尝试分别作出了△BDC,△AEC中
的数量关系仍然成立,并尝试分别作出了△BDC,△AEC中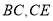 边上的高,请你证明小明的猜想。
边上的高,请你证明小明的猜想。
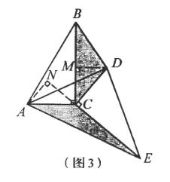
(1)DE∥AC;S1=S2;(2)证明见解析.
【解析】
试题分析:(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=
12AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明.
试题解析:(1)①DE∥BC
理由如下:
∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°-∠B=90°-30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=AC=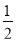 AB,
AB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(2)如图,∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
 ,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2.
考点: 1.全等三角形的判定与性质;2.平行线的判定;3.等边三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2015届江苏无锡市八年级下学期期中考试数学卷(解析版) 题型:解答题
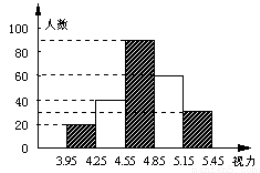
初中生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:
(1)本次调查共抽测了 名学生,占该市初中生总数的百分比是 ;
(2)从左到右五个小组的频率之比是 ;
(3)如果视力在4.9以上(含4.9)均属正常,则全市有 名初中生的视力正常, 视力正常的合格率是 .
查看答案和解析>>
科目:初中数学 来源:2015届江苏无锡前洲中学八年级3月阶段练习数学试卷(解析版) 题型:选择题
如图,下列说法正确的是( )
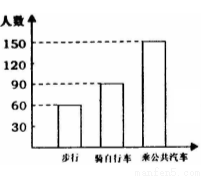
A.步行人数最少只为90人
B.坐公共汽车的人数占总数的50%
C.步行人数为50人
D.步行与骑自行车的人数和比坐公共汽车的人数要少
查看答案和解析>>
科目:初中数学 来源:2015届江苏宜兴和桥学区八年级下学期期中考试数学试卷(解析版) 题型:填空题
下列4个事件:①异号两数相加,和为负数;②异号两数相减,差为正数;③异号两数相乘,积为正数;④异号两数相除,商为负数.必然事件是 ,不可能事件是 .(将事件的序号填上即可)
查看答案和解析>>
科目:初中数学 来源:2015届江苏宜兴和桥学区八年级下学期期中考试数学试卷(解析版) 题型:选择题
已知四边形ABCD是平行四边形,下列结论中不正确的是 ( )
A.当AB=BC时,它是菱形 B.当∠ABC=90°时,它是矩形
C.当AC=BD时,它是正方形 D.当AC⊥BD时,它是菱形
查看答案和解析>>
科目:初中数学 来源:2015届广东省深圳市石岩公学八年级3月质量检测数学试卷(解析版) 题型:解答题
解不等式:(1) 8x+1<6x-3 (2)解不等式:5x-9<3(x+1)
(3)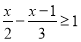 (4)
(4)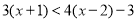
查看答案和解析>>
科目:初中数学 来源:2015届广东省深圳市石岩公学八年级3月质量检测数学试卷(解析版) 题型:选择题
如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( )

A.30° B.36° C.45° D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com