
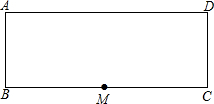
 如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.
如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm. 分析 过F作ME⊥AD于E,可得出四边形ABME为矩形,利用矩形的性质得到AE=BF,AB=EM,分两种情况考虑:(i)当G在AB上,B′落在AE上时,如图1所示,由折叠的性质得到B′M=BM,BG=B′G,在直角三角形EMB′中,利用勾股定理求出B′E的长,由AE-B′E求出AB′的长,设AG=x,由AB-AG表示出BG,即为B′G,在直角三角形AB′G中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出AG的长,进而求出BG的长,在直角三角形GBM中,利用勾股定理即可求出折痕MG的长;(ii)当G在AE上,B′落在ED上,如图2所示,同理求出B′E的长,设A′G=AG=y,由AE+B′E-AG表示出GB′,在直角三角形A′B′G中,利用勾股定理列出关于y的方程,求出方程的解得到y的值,求出AG的长,由AE-AG求出GE的长,在直角三角形GEM中,利用勾股定理即可求出折痕MG的长,综上,得到所有满足题意的折痕MG的长.
解答 解:分两种情况考虑:
(i)如图1所示,过M作ME⊥AD于E,G在AB上,B′落在AE上,可得四边形ABME为矩形,
∴EM=AB=16,AE=BM,
又∵BC=40,M为BC的中点,
∴由折叠可得:B′M=BM=$\frac{1}{2}$BC=20,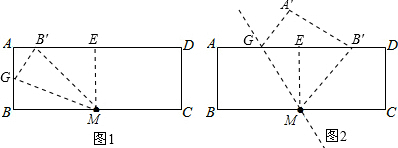
在Rt△EMB′中,根据勾股定理得:B′E=$\sqrt{B′{M}^{2}-E{M}^{2}}$=12,
∴AB′=AE-B′E=20-12=8,
设AG=x,则有GB′=GB=16-x,
在Rt△AGB′中,根据勾股定理得:GB′2=AG2+A′B′2,
即(16-x)2=x2+82,
解得:x=6,
∴GB=16-6=10,
在Rt△GBM中,根据勾股定理得:GM=$\sqrt{G{B}^{2}+B{M}^{2}}$=10$\sqrt{5}$;
(ii)如图2所示,过M作ME⊥AD于E,G在AE上,B′落在ED上,可得四边形ABME为矩形,
∴EM=AB=16,AE=BM,
又BC=40,M为BC的中点,
∴由折叠可得:B′M=BM=$\frac{1}{2}$BC=20,
在Rt△EMB′中,根据勾股定理得:B′E=$\sqrt{B′{M}^{2}-E{M}^{2}}$=12,
∴AB′=AE+B′E=20+12=32,
设AG=A′G=y,则GB′=AB′-AG=AE+EB′-AG=32-y,A′B′=AB=16,
在Rt△A′B′G中,根据勾股定理得:A′G2+A′B′2=GB′2,
即y2+162=(32-y)2,
解得:y=12,
∴AG=12,
∴GE=AE-AG=20-12=8,
在Rt△GEM中,根据勾股定理得:GM=$\sqrt{G{E}^{2}+E{M}^{2}}$=8$\sqrt{5}$;
综上所述,折痕MG=10$\sqrt{5}$或8$\sqrt{5}$.
故答案为:10$\sqrt{5}$或8$\sqrt{5}$.
点评 此题考查了翻折变换-折叠问题,矩形的判定与性质,勾股定理,利用了方程、转化及分类讨论的思想,是一道综合性较强的试题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 度量三角形的内角和,结果是360° | B. | 射击运动员射击一次,命中9环 | ||
| C. | 明天会下雨 | D. | 买一张电影票,座位号是奇数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
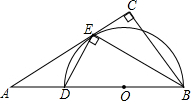 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{12}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
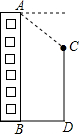 如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为11.6m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为11.6m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
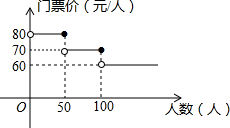 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com