
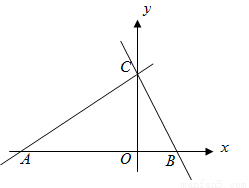
(13分)如图,在△ABC中,∠ACB=90°,CD⊥AB,

(1)图中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如下图),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为 秒是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点
秒是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)3对,分别是:△ABC∽△ACD, △ABC∽△CBD , △ACD∽△CBD;(2)4.8;(3)存在,(1.35,3)或(3.15,1.8).
【解析】
试题分析:(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到 AB•CD=
AB•CD= AC•BC,即可求出CD的长;
AC•BC,即可求出CD的长;
(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.
试题解析:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,∴BC= =6.
=6.
∵△ABC的面积= AB•CD=
AB•CD= AC•BC,∴CD=
AC•BC,∴CD= =4.8;
=4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=6,OC=4.8,∴OB= =3.6.
=3.6.
分两种情况:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴ ,∴
,∴ ,解得t=2.25,即BQ=CP=2.25,
,解得t=2.25,即BQ=CP=2.25,
∴OQ=OB﹣BQ=3.6﹣2.25=1.35,BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ= =
= ,∴点P的坐标为(1.35,3);
,∴点P的坐标为(1.35,3);

②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,∴ ,∴
,∴ ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,∴ ,∴
,∴ ,∴PE=1.8.
,∴PE=1.8.
在△BPE中,BE= =
= ,∴OE=OB﹣BE=3.6﹣0.45=3.15,
,∴OE=OB﹣BE=3.6﹣0.45=3.15,
∴点P的坐标为(3.15,1.8);
综上可得,点P的坐标为(1.35,3)或(3.15,1.8).

考点:1.相似三角形的判定与性质;2.勾股定理.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源:2014-2015学年福建省南平市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )

A.SSS B.SAS C.AAS D.ASA
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省泉州市惠安第三教研片区九年级上学期期中考试数学试卷(解析版) 题型:选择题
若二次根式 有意义,则
有意义,则 的取值范围是( )
的取值范围是( )
A. B.
B.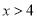 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省泉州市惠安第三教研片区九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知△ABC与△DEF相似且相似比为2:3,则△ABC与△DEF的面积比是________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省漳州立人学校八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列是有理数的是( )
A.0
B.
C.
D.1.010010001…(每两个1之间的0的个数依次多1)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省漳州立人学校八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)

(1)作△A′B′C′,使△ABC与△A′B′C′关于x轴对称;
(2)AB长度是 (填“有理数”或“无理数”) ,BC= ;
(3)△ABC 直角三角形(填“是”或“不是”);
(4)△ABC的面积= 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com