
【题目】为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积(平方米) | 单价(万元/平方米) |
不超过30(平方米) | 0.3 |
超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
【答案】(1)42(万元)
(2)由题意,得
①当0≤x≤30时,y=0.9x;
②当30<x≤m时,y=1.5x﹣18;
③当x>m时,∴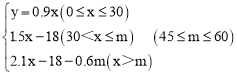 。
。
(3)45≤m<50
【解析】
(1)根据房款=房屋单价×购房面积就可以表示出应缴房款。
(2)由分段函数当0≤x≤30,当30<x≤m时,当x>m时,分别求出y与x之间的表达式即可。
(3)当50≤m≤60和当45≤m<50时,分别讨论建立不等式组就可以求出结论。
解:(1)由题意,得
三口之家应缴购房款为:0.3×90+0.5×30=42(万元)。
(2)由题意,得
①当0≤x≤30时,y=0.3×3x=0.9x;
②当30<x≤m时,y=0.9×30+0.5×3×(x﹣30)=1.5x﹣18;
③当x>m时,y=0.3×30+0.5×3(m﹣30)+0.7×3×(x﹣m)=2.1x﹣18﹣0.6m;
∴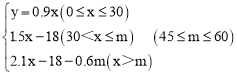 。
。
(3)由题意,得
①当50≤m≤60时,y=1.5×50﹣18=57(舍)。
②当45≤m<50时,y=2.1×50 0.6m﹣18=87﹣0.6m,
∵57<y≤60,∴57<87﹣0.6m≤60,∴45≤m<50。
综合①②得45≤m<50。


科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF,
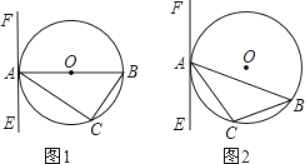
(1)如图1,若AB为直径,要使得EF是⊙O的切线,还需要添加的条件是(只须写出两种不同情况)① 或② .
(2)如图2,若AB为非直径的弦,∠CAE=∠B,试说明EF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中抛物线与x轴的正半轴交于点![]() ,交y于点C,顶点
,交y于点C,顶点![]() ,直线AB与y轴交于点D.
,直线AB与y轴交于点D.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 联结BC,如果点P在x轴上,且
联结BC,如果点P在x轴上,且![]() 与
与![]() 相似,求出点P坐标.
相似,求出点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
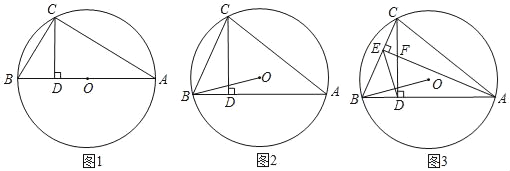
【题目】如图所示,![]() 内接于圆O,
内接于圆O,![]() 于D;
于D;
(1)如图1,当AB为直径,求证:![]() ;
;
(2)如图2,当AB为非直径的弦,连接OB,则(1)的结论是否成立?若成立请证明,不成立说明由;
(3)如图3,在(2)的条件下,作![]() 于E,交CD于点F,连接ED,且
于E,交CD于点F,连接ED,且![]() ,若
,若![]() ,
,![]() ,求CF的长度.
,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆锥的底面半径为10 cm,高为10![]() cm.
cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
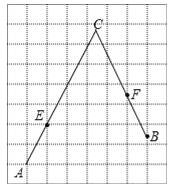
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。
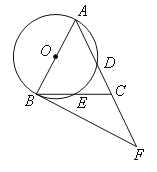
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com