
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。
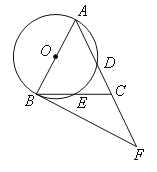
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
【答案】解:(1)如图,连接AE,
∵AB是⊙O的直径,
∴∠AEB=900,即AE⊥BC。
又∵AB=AC,∴BE=CE。
(2)∵∠BAC=540,AB=AC,∴∠ABC=630。
又∵BF是⊙O的切线,∴∠ABF=900。
∴∠CBF=∠ABF一∠ABC=270。
(3)连接OD,

∵OA=OD,∠BAC=540,∴∠AOD=720。
又∵AB=6,∴OA=2。
∴![]() 。
。
【解析】(1)连接AE,则根据直径所对圆周角是直角的性质得AE⊥BC,从而根据等腰三角形三线合一的性质得出结论。
(2)由∠BAC=540,AB=AC,根据等腰三角形等边对等角的性质和三角形内角和等于零180度求得∠ABC=630;由切线垂直于过切点直径的性质得∠ABF=900,从而由∠CBF=∠ABF一∠ABC得出结论。
(3)连接OD,根据同弧所对圆周角是圆心角一半的性质,求得∠AOD=720,根据弧长公式即可求。


科目:初中数学 来源: 题型:
【题目】为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积(平方米) | 单价(万元/平方米) |
不超过30(平方米) | 0.3 |
超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
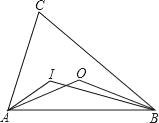
A. ∠AIB=∠AOBB. ∠AIB≠∠AOB
C. 2∠AIB﹣![]() ∠AOB=180°D. 2∠AOB﹣
∠AOB=180°D. 2∠AOB﹣![]() ∠AIB=180°
∠AIB=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线![]() 与
与![]() 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线![]() 的对称点恰好是点M,求
的对称点恰好是点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
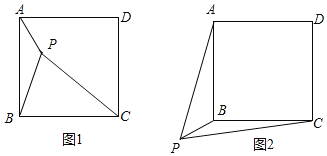
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
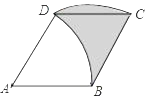
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
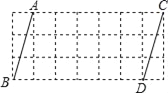
【题目】如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A,B,C,D均在小正方形顶点上.
(1)在方格纸中画出面积为5的等腰直角△ABE,且点E在小正方形的顶点上;
(2)在方格纸中画出面积为3的等腰△CDF,其中CD为一腰,且点F在小正方形的顶点上;
(3)在(1)(2)条件下,连接EF,请直接写出线段EF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)经过点(﹣1,0),且满足4a+2b+c>0,有下列结论:①a+b>0;②﹣a+b+c>0;③b2﹣2ac>5a2.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com