
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
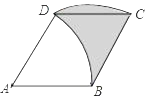
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
【答案】B
【解析】
连接BD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠ABD=60°,再求出∠CBD=60°,DB=BC=AD,从而确定S扇形BDC=S扇形ABD,然后求出阴影部分的面积=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD,计算即可得解.
解:如图,连接BD,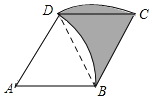
∵四边形ABCD是菱形,
∴AB=AD=BC,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,AD=DB=BC=4
又∵菱形的对边AD∥BC,
∴∠CBD=∠ADB=60°,
∴S扇形BDC=S扇形ABD
∴S阴影=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD=![]() =4
=4![]() cm2.
cm2.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图所示,![]() 内接于圆O,
内接于圆O,![]() 于D;
于D;
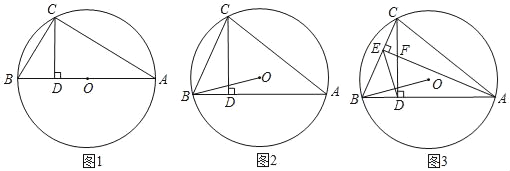
(1)如图1,当AB为直径,求证:![]() ;
;
(2)如图2,当AB为非直径的弦,连接OB,则(1)的结论是否成立?若成立请证明,不成立说明由;
(3)如图3,在(2)的条件下,作![]() 于E,交CD于点F,连接ED,且
于E,交CD于点F,连接ED,且![]() ,若
,若![]() ,
,![]() ,求CF的长度.
,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
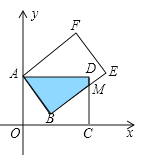
(1)求AD的长;
(2)求阴影部分的面积和直线AM的解析式;
(3)求经过A、B、D三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
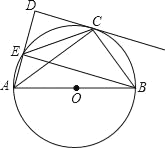
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,AD交⊙O于点E,AC平分∠BAD,连接BE.
(1)求证:CD⊥ED;
(2)若CD=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。
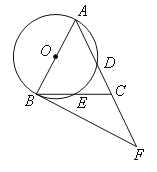
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:
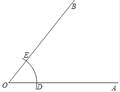
已知:∠AOB.
求作:射线OC,使它平分∠AOB.
作法:
(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D、E为圆心,大于![]() DE的同样长为半径作弧,两弧相交于点C;
DE的同样长为半径作弧,两弧相交于点C;
(3)作射线OC.
所以射线OC就是所求作的射线.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连结CE,CD.
∵OE=OD, = ,OC=OC,
∴△OEC≌△ODC(依据: ),
∴∠EOC=∠DOC,
即OC平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
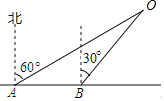
【题目】如图,某轮船在海上向正东方向航行,上午8:00在点A处测得小岛O在北偏东60°方向的16![]() km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
(1)求轮船从A处到B处的航速;
(2)如果轮船按原速继续向东航行,还需经过多少时间轮船才恰好位于小岛的东南方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
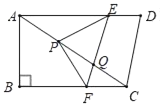
【题目】如图,四边形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.点P以每秒5个单位长度由点A沿线段AC运动;同时,线段EF以相同的速度由CD出发沿DA方向平移,与AC交于点Q,连结PE,PF.当点F与点B重合时,停止所有运动,设P运动时间为t秒.
(1)求证:△APE≌△CFP.
(2)当t<1时,若△PEF为直角三角形,求t的值.
(3)作△PEF的外接圆⊙O.
①当⊙O只经过线段AC的一个端点时,求t的值.
②作点P关于EF的对称点P′,当P′落在CD上时,请直接写出线段CP′的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com