
【题目】(12分)矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
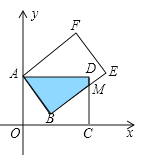
(1)求AD的长;
(2)求阴影部分的面积和直线AM的解析式;
(3)求经过A、B、D三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)7;(2)16,![]() ;(3)
;(3)![]() ;(4)P(3,1)、(
;(4)P(3,1)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).
【解析】
试题(1)作BP⊥AD于P,BQ⊥MC于Q,如图1,由旋转的性质得AB=AO=5,BE=OC=AD,∠ABE=90°,得到∠ABP=∠MBQ,可证明Rt△ABP∽Rt△MBQ得到![]() ,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y﹣2,利用比例性质得到PBMQ=xy,而PB﹣MQ=DQ﹣MQ=DM=1,利用完全平方公式和勾股定理解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y﹣2,利用比例性质得到PBMQ=xy,而PB﹣MQ=DQ﹣MQ=DM=1,利用完全平方公式和勾股定理解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
(2)由AB=BM可得到Rt△ABP≌Rt△MBQ,则BQ=PD=7﹣AP,MQ=AP,利用勾股定理可得到MQ=3,则BQ=4,根据三角形面积公式和梯形面积公式,利用S阴影部分=S梯形ABQD﹣S△BQM进行计算即可;然后利用待定系数法求直线AM的解析式;
(3)先确定B(3,1),然后利用待定系数法求抛物线的解析式;
(4)设P(x,y),则点P(x,y)到直线AM的距离为: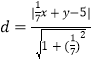 =
=![]() ,而AM=
,而AM=![]() ,由
,由![]() =
=![]() AMd=
AMd=![]() =
=![]() ,得到
,得到![]() ,由
,由![]() ,得到
,得到![]() ,即
,即![]() 或
或![]() ,解方程即可得到点P的坐标.
,解方程即可得到点P的坐标.
试题解析:(1)作BP⊥AD于P,BQ⊥MC于Q,如图1,∵矩形AOCD绕顶点A(0,5)逆时针方向旋转得到矩形ABEF,∴AB=AO=5,BE=OC=AD,∠ABE=90°,∵∠PBQ=90°,∴∠ABP=∠MBQ,∴Rt△ABP∽Rt△MBQ,∴![]() ,设BQ=PD=x,AP=y,则AD=x+y,BM=x+y﹣2,∴
,设BQ=PD=x,AP=y,则AD=x+y,BM=x+y﹣2,∴![]() ,∴PBMQ=xy,∵PB﹣MQ=DQ﹣MQ=DM=1,∴
,∴PBMQ=xy,∵PB﹣MQ=DQ﹣MQ=DM=1,∴![]() ,即
,即![]() ,∴
,∴![]() ,解得x+y=7,∴BM=5,∴BE=BM+ME=5+2=7,∴AD=7;
,解得x+y=7,∴BM=5,∴BE=BM+ME=5+2=7,∴AD=7;
(2)∵AB=BM,∴Rt△ABP≌Rt△MBQ,∴BQ=PD=7﹣AP,MQ=AP,∵![]() ,∴
,∴![]() ,解得MQ=4(舍去)或MQ=3,∴BQ=7﹣3=4,∴S阴影部分=S梯形ABQD﹣S△BQM=
,解得MQ=4(舍去)或MQ=3,∴BQ=7﹣3=4,∴S阴影部分=S梯形ABQD﹣S△BQM=![]() ×(4+7)×4﹣
×(4+7)×4﹣![]() ×4×3=16;
×4×3=16;
设直线AM的解析式为![]() ,把A(0,5),M(7,4)代入得:
,把A(0,5),M(7,4)代入得:![]() ,解得:
,解得: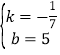 ,∴直线AM的解析式为
,∴直线AM的解析式为![]() ;
;
(3)设经过A、B、D三点的抛物线的解析式为![]() ,∵AP=MQ=3,BP=DQ=4,∴B(3,1),而A(0,5),D(7,5),∴
,∵AP=MQ=3,BP=DQ=4,∴B(3,1),而A(0,5),D(7,5),∴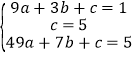 ,解得:
,解得: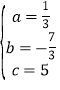 ,∴经过A、B、D三点的抛物线的解析式为
,∴经过A、B、D三点的抛物线的解析式为![]() ;
;
(4)存在.∵A(0,5),M(7,4),∴AM=![]() ,设P(x,y),则点P(x,y)到直线AM的距离为:
,设P(x,y),则点P(x,y)到直线AM的距离为: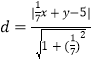 =
=![]() ,∵
,∵![]() =
=![]() AMd=
AMd=![]() =
=![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,
,
由![]() ,解得:
,解得:![]() ,
,![]() ,此时P点坐标为(3,1)、(
,此时P点坐标为(3,1)、(![]() ,
,![]() );
);
由![]() ,解得:
,解得:![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
综上所述,点P的坐标为(3,1)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
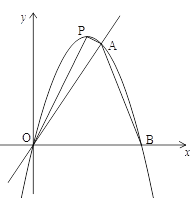
【题目】如图,抛物线y=ax2+bx的顶点为P(2,4),直线y=![]() x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
(1)求抛物线的解析式和点A的坐标;
(2)求四边形APOB的面积;
(3)M是抛物线上位于直线y=![]() x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
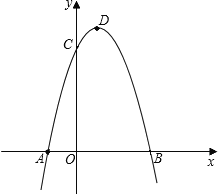
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
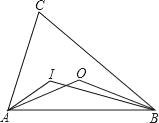
A. ∠AIB=∠AOBB. ∠AIB≠∠AOB
C. 2∠AIB﹣![]() ∠AOB=180°D. 2∠AOB﹣
∠AOB=180°D. 2∠AOB﹣![]() ∠AIB=180°
∠AIB=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
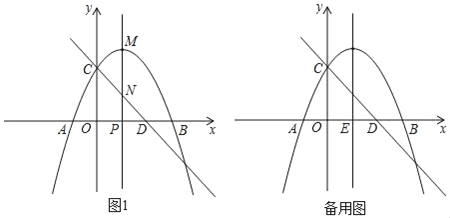
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .动点
.动点![]() 在抛物线上运动,过点
在抛物线上运动,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在线段
在线段![]() 上时,
上时,![]() 的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
(3)点![]() 是抛物线对称轴与
是抛物线对称轴与![]() 轴的交点,点
轴的交点,点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 在运动过程中,若以
在运动过程中,若以![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线![]() 与
与![]() 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线![]() 的对称点恰好是点M,求
的对称点恰好是点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
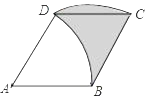
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com