
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
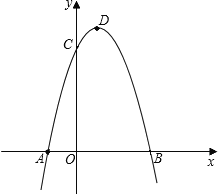
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
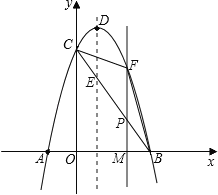
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
【答案】(1)A(﹣1,0),B(3,0),C(0,3).抛物线的对称轴是:直线x=1.
(2)①当m=2时,四边形PEDF为平行四边形.②S=﹣![]() m2+
m2+![]() m(0≤m≤3).
m(0≤m≤3).
【解析】
试题分析:(1)已知了抛物线的解析式,当y=0时可求出A,B两点的坐标,当x=0时,可求出C点的坐标.根据对称轴x=﹣![]() 可得出对称轴的解析式.
可得出对称轴的解析式.
(2)PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.
根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
(3)可将三角形BCF分成两部分来求:
一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.
一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.
然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式.
解:(1)A(﹣1,0),B(3,0),C(0,3).
抛物线的对称轴是:直线x=1.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:![]()
解得:![]() .
.
所以直线BC的函数关系式为:y=﹣x+3.
当x=1时,y=﹣1+3=2,
∴E(1,2).
当x=m时,y=﹣m+3,
∴P(m,﹣m+3).
在y=﹣x2+2x+3中,当x=1时,y=4.
∴D(1,4)
当x=m时,y=﹣m2+2m+3,
∴F(m,﹣m2+2m+3)
∴线段DE=4﹣2=2,
线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形.
由﹣m2+3m=2,
解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M,由B(3,0),O(0,0),
可得:OB=OM+MB=3.
∵S=S△BPF+S△CPF
即S=![]() PFBM+
PFBM+![]() PFOM=
PFOM=![]() PF(BM+OM)=
PF(BM+OM)=![]() PFOB.
PFOB.
∴S=![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣![]() m2+
m2+![]() m(0≤m≤3).
m(0≤m≤3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
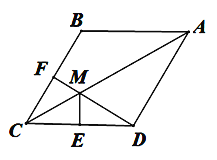
【题目】(本题满分10分)如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E, ∠BAC=∠CDF.
(1)求证BC=2CE;
(2)求证AM=DF+ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
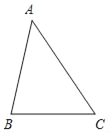
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E.
(1)尺规作图作出AB的垂直平分线DE,并连结BD;(保留作图痕迹,不写作法)
(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点.
(1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.
(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com