
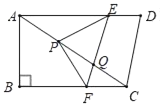
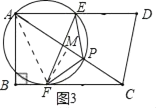
【题目】如图,四边形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.点P以每秒5个单位长度由点A沿线段AC运动;同时,线段EF以相同的速度由CD出发沿DA方向平移,与AC交于点Q,连结PE,PF.当点F与点B重合时,停止所有运动,设P运动时间为t秒.
(1)求证:△APE≌△CFP.
(2)当t<1时,若△PEF为直角三角形,求t的值.
(3)作△PEF的外接圆⊙O.
①当⊙O只经过线段AC的一个端点时,求t的值.
②作点P关于EF的对称点P′,当P′落在CD上时,请直接写出线段CP′的长.
【答案】(1)详见解析;(2)t=![]() ;(3)①t的值为
;(3)①t的值为![]() 和
和![]() ;②
;②![]()
【解析】
(1)利用勾股定理求出AD=AC=10,根据AD∥BC得到∠EAC=∠ACF,再根据AE=CP=10﹣5t即可证得结论;
(2)过点P作PM⊥AD于点M,延长MP交BC于N,证明四边形ABNM是矩形得到△PNC∽△ABC,求出PM=MN﹣PN=3t,NF=NC﹣FC=8﹣9t,由△APE≌△CFP得到PE=PF,由△EPF为直角三角形得到∠MEP=∠NPF,由此证明△EMP≌△PNF得到PM=NF,建立等式求出t;
(3)①分两种情况:当⊙O过点C时,连接CE,过点E作EM⊥AC于M.根据PE=PF证得∠PCE=∠PCF,再求出CE=AE=10﹣5t,CM=AM=![]() AC=5,根据cos∠PCE=cos∠PCF即可求出t;当⊙O过点A时可得AF=FC=5t,根据cos∠PCE=cos∠PCF即可求出t;
AC=5,根据cos∠PCE=cos∠PCF即可求出t;当⊙O过点A时可得AF=FC=5t,根据cos∠PCE=cos∠PCF即可求出t;
②过点C作CH⊥AD于H,连接PP',交EF于点G,证明△PGQ∽△PP'C求出PQ,根据对顶角的性质及平行线的性质求出CQ=CF求出t,利用勾股定理求出EF,计算出FG、FQ求出QG即可求出答案.
解:(1)证明:∵AD∥BC,EF∥CD
∴四边形CDEF是平行四边形,∠EAC=∠ACF
∴ED=FC=5t
∵∠B=90°,AB=6,BC=8
∴AD=AC=![]() =10
=10
∴AE=CP=10﹣5t
在△APE与△CFP中,

∴△APE≌△CFP(SAS)
(2)过点P作PM⊥AD于点M,延长MP交BC于N,
∴∠EMP=∠PNF=90°,MN∥AB
∴∠MEP+∠MPE=90°,四边形ABNM是矩形,△PNC∽△ABC
∴MN=AB=6,![]()
∴PN=6﹣3t,NC=8﹣4t
∴PM=MN﹣PN=3t,NF=NC﹣FC=8﹣9t
∵△APE≌△CFP
∴PE=PF,
∵△EPF为直角三角形
∴∠EPF=90°
∴∠MPE+∠NPF=90°
∴∠MEP=∠NPF
在△EMP与△PNF中,
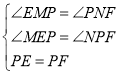
∴△EMP≌△PNF(AAS)
∴PM=NF
∴3t=8﹣9t
解得:t=![]()
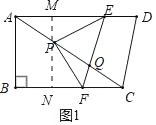
(3)①(ⅰ)当⊙O过点C时(如图2),连接CE,过点E作EM⊥AC于M.
∵PE=PF,
∴![]()
∴∠PCE=∠PCF
∵AD∥BC
∴∠PCF=∠DAC
∴∠PCE=∠DAC,
∴CE=AE=10﹣5t,CM=AM=![]() AC=5
AC=5
∵cos∠PCE=cos∠PCF
∴![]() 即
即![]()
解得:t=![]()
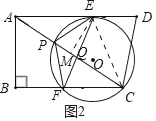
(ⅱ)当⊙O过点A时(如图3),可得AF=FC=5t
∴cos∠FAP=cos∠PCF
∴![]() 即
即![]()
解得:t=![]()
综上所述,t的值为![]() 和
和![]()
②过点C作CH⊥AD于H,连接PP',交EF于点G
∴G为PP'和EF的中点
∵P'在CD上,EF∥CD
∴△PGQ∽△PP'C
∴![]() =
=![]()
∴PQ=CQ=![]() PC=
PC=![]()
∵AC=AD
∴∠ACD=∠D
∴∠AQE=∠ACD=∠D=∠AEQ
∵∠AQE=∠CQF,∠AEQ=∠CFQ
∴∠CQF=∠CFQ
∴CQ=CF
∴![]()
解得:t=![]()
∴CF=![]() ,AE=10﹣
,AE=10﹣![]() =
=![]()
∴![]() ,即FQ=
,即FQ=![]() EF
EF
∵∠CHD=90°,CH=AB=6,DH=AD﹣AH=AD﹣BC=2
∴EF=CD=![]()
∴FG=![]() EF=
EF=![]() ,FQ=
,FQ=![]() EF=
EF=![]()
∴GQ=FG﹣FQ=![]()
∴CP'=2GQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
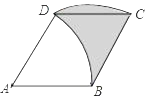
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小涛根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
请直接写出:![]() =, m=, n=;
=, m=, n=;
(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数![]() 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)
(4)请结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,直接写出
有三个不同的解,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
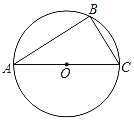
【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2![]() .
.
(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:
(1)一套“福娃”玩具和一枚徽章的价格各是多少元?
(2)买5套“福娃”玩具和10枚徽章共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人自主学习的选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
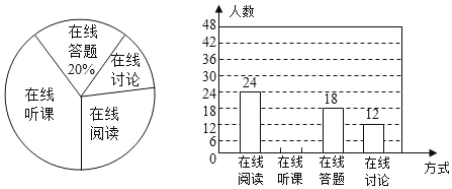
请你根据统计图中提供的信息解答下列问题:
(1)求本次调查的学生总人数;
(2)通过计算补全条形统计图;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生有多少人.
人,请你估计该校对在线阅读最感兴趣的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
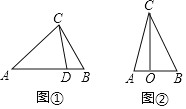
【题目】如图①在![]() 中,若点
中,若点![]() 在边
在边![]() 上,且
上,且![]() 则点
则点![]() 定义为
定义为![]() 的边
的边![]() 上的“金点”.
上的“金点”.
![]() 已知点
已知点![]() 是
是![]() 的边
的边![]() 上的“金点”:
上的“金点”:
①若![]() 则
则![]() 的长为 _;
的长为 _;
②若![]() 则
则![]() 的长为 _;
的长为 _;
![]() 在图①中,若点
在图①中,若点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 试判断点
试判断点![]() 是不是
是不是![]() 的“金
的“金
点”,并说明理由;
![]() 如图②,已知点
如图②,已知点![]() 为同一直线上三点,且
为同一直线上三点,且![]() 在
在![]() 所在直线上是否存在一点
所在直线上是否存在一点![]() 使点
使点![]() 中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段
中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com