
【题目】已知△ABC内接于⊙O,过点A作直线EF,
(1)如图1,若AB为直径,要使得EF是⊙O的切线,还需要添加的条件是(只须写出两种不同情况)① 或② .
(2)如图2,若AB为非直径的弦,∠CAE=∠B,试说明EF是⊙O的切线.
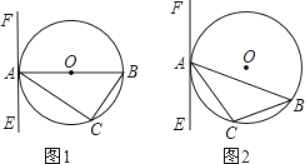
【答案】(1)①EF⊥AB,②∠EAC=∠B; (2)证明见解析.
【解析】
(1)添加条件EF⊥AB,根据切线的判定推出即可;添加条件∠EAC=∠B,根据直径推出∠CAB+∠B=90°,推出∠EAC+∠CAB=90°,根据切线判定推出即可;
(2)作直径AM,连接CM,推出∠M=∠B=∠EAC,求出∠EAC+∠CAM=90°,根据切线的判定推出即可.
(1)添加的条件是①EF⊥AB,
理由是∵EF⊥AB,OA是半径,
∴EF是⊙O的切线;
②∠EAC=∠B,
理由是:∵AB是⊙O的直径,
∴∠C=90°,
∴∠B+∠CAB=90°,
∵∠EAC=∠B,
∴∠EAC+∠CAB=90°,
∴EF⊥AB,
∵OA是半径,
∴EF是⊙O的切线;
(2)
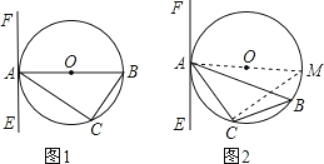
作直径AM,连接CM,
即∠B=∠M(在同圆或等圆中,同弧所对的圆周角相等),
∵∠EAC=∠B,
∴∠EAC=∠M,
∵AM是⊙O的直径,
∴∠ACM=90°,
∴∠CAM+∠M=90°,
∴∠EAC+∠CAM=90°,
∴EF⊥AM,
∵OA是半径,
∴EF是⊙O的切线.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() (a、b、c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①当
(a、b、c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①当![]() 时,
时,![]() ;②
;②![]() ;③
;③![]() ;④3a+c>0,其中正确的是( )
;④3a+c>0,其中正确的是( )
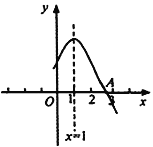
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①abc<0;②b2﹣4ac>0;③3a+c<0;④(a+c)2<b2,⑤a+b+c>0
其中正确的序号是_____.
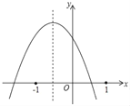
查看答案和解析>>
科目:初中数学 来源: 题型:
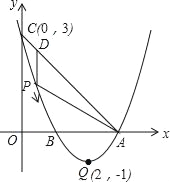
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )

A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积(平方米) | 单价(万元/平方米) |
不超过30(平方米) | 0.3 |
超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
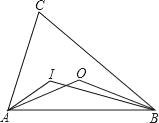
A. ∠AIB=∠AOBB. ∠AIB≠∠AOB
C. 2∠AIB﹣![]() ∠AOB=180°D. 2∠AOB﹣
∠AOB=180°D. 2∠AOB﹣![]() ∠AIB=180°
∠AIB=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com