
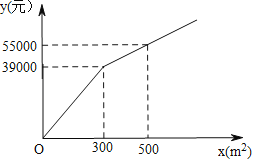
����Ŀ��Ϊ�����������������˾ӳ��У���������һ���㳡����ֲ�ס������ֻ��ܣ����г����飬���ֻ��ܵ���ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ��
��1��ֱ��д����0��x��300��x��300ʱ��y��x�ĺ�����ϵʽ��
��2��������ֲ���Ϊ200m2ʱ��������ֲ�ס������ֻ��ܵķ��ã�
��3���㳡�ϼס������ֻ��ܵ���ֲ�����1200m2�������ֻ��ܵ���ֲ���������200m2���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
���𰸡���1��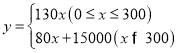 ����2����20000Ԫ����26000Ԫ����3�����ֻ�����ֲ���Ϊ400m2�����ֻ�����ֲ���Ϊ800m2��119000Ԫ
����2����20000Ԫ����26000Ԫ����3�����ֻ�����ֲ���Ϊ400m2�����ֻ�����ֲ���Ϊ800m2��119000Ԫ
��������
��1����ͼ��֪y��x�ĺ�����ϵʽ�Ƿֶκ���������ϵ���������ʽ���ɣ�
��2������ֵ���루1���Ľ��ۼ��ɽ��
��3�������ֻ�����ֲΪ am2������ֻ�����ֲ��1200��a��m2������ʵ���������ȷ��a�ķ�Χ�������ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ���Է����������ٷ���Ϊ���٣�
��1����0��x��300ʱ����y=k1x����������ã�
300k1=39000�����k1=130����y=130x��
��x��300ʱ����y=k2x+b����������ã�
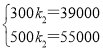 �����
�����![]() ����y=80x+15000��
����y=80x+15000��
��y=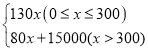 ��
��
��2����ֲ���ֻ��ܵķ���Ϊ��200��100��20000Ԫ����ֲ���ֻ��ܵķ���Ϊ200��130��26000Ԫ��
��3�����ܷ���ΪW�����ֻ�����ֲ���Ϊam2������ֻ�����ֲ���Ϊ��1200��a��m2��������ã�200��a��2��1200��a������200��a��800��
��200��a��300ʱ��
W��130a+100��1200��a����30a+120000��
�ʵ�x��200ʱ��Wmin��126000��
��300��a��800ʱ��
W��80a+15000+100��1200��a������20a+135000��
�ʵ�a��800ʱ��Wmin��119000��
��119000��126000���൱a��800ʱ�ܷ������٣�
�𣺵����ֻ�����ֲ���Ϊ400m2�����ֻ�����ֲ���Ϊ800m2ʱ����ֲ�ܷ������٣������ܷ���Ϊ119000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������a1��a2��a3��ƽ����Ϊ4������Ϊ3����ô����a1+2��a2+2��a3+2��ƽ�����ͷ���ֱ��ǣ�������
A. 4��3B. 6��3C. 3��4D. 6��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC�Ǿ��Σ�������ODE�У�OE��DE����A��D��x����������ϣ���C��y����������ϣ���B��E�ڷ���������y��![]() ��ͼ���ϣ�OA��5��OC��1�����ODE�����Ϊ��������
��ͼ���ϣ�OA��5��OC��1�����ODE�����Ϊ��������
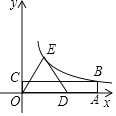
A.2.5B.5C.7.5D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2013���Ĵ��ϳ�3�֣���ͼ���Ѿ���ABCD��EF���ۣ���Bǡ������AD�ߵ�B�䴦����AE=2��DE=6����EFB=60�㣬�����ABCD������ǡ� ��
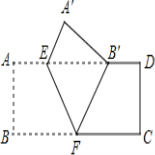
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2��bx��c��x�ύ��A��B���㣨A����B����ࣩ����y�ύ�ڵ�C��0����3�����Գ�����ֱ��x=1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽�CE�ڵ�F������������P��Q���㣬�ҵ�P�ڵ������ޣ�
�ٵ��߶�PQ=![]() ABʱ����tan��CED��ֵ��
ABʱ����tan��CED��ֵ��
�ڵ��Ե�C��D��EΪ�������������ֱ��������ʱ����ֱ��д����P�����꣮
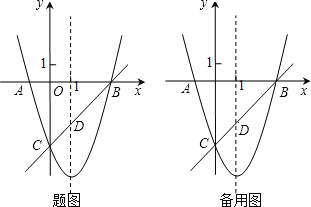
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAD���ֱ�BC��BD�ڵ�E��P������OE����ADC=60�㣬AB=![]() BC=1�������н��ۣ�
BC=1�������н��ۣ�
�١�CAD=30����BD=![]() ��Sƽ���ı���ABCD=ABAC��OE=
��Sƽ���ı���ABCD=ABAC��OE=![]() AD��S��APO=
AD��S��APO=![]() ����ȷ�ĸ����ǣ�������
����ȷ�ĸ����ǣ�������

A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABCD�Ķ���A���������ֱ��AP����B����ֱ��AP�ĶԳƵ�ΪE������BE��DE������DE��ֱ��AP�ڵ�F��
��1�������ⲹȫͼ1��
��2������PAB��30�㣬���ADF�Ķ�����
��3����ͼ����45�㣼��PAB��90�㣬�õ�ʽ��ʾ�߶�AB��FE��FD֮���������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����CD���ң�AB��CD������ΪE����P����O�ϣ�����BP��PD��BC����CD=![]() ��sinP=
��sinP=![]() ������O��ֱ��Ϊ��������
������O��ֱ��Ϊ��������

A. 8 B. 6 C. 5 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע����Ӫ��ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺

��1�������ʾ������ѧ������_______�ˣ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ_______����
��2���벹ȫ����ͳ��ͼ��
��3��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ���������
��4�����Ӷ�У��ȫ֪ʶ�ﵽ���˽����̶ȵ�3��Ů����2�������������ȡ2�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com