
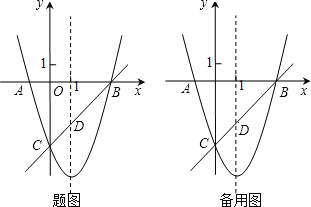
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=![]() AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
【答案】(1)抛物线的函数表达式为y=x2-2x-3.(2)直线BC的函数表达式为y=x-3.(3)①![]() .①P1(1-
.①P1(1-![]() ,-2),P2(1-
,-2),P2(1-![]() ,
,![]() ).
).
【解析】
已知C点的坐标,即知道OC的长,可在直角三角形BOC中根据∠BCO的正切值求出OB的长,即可得出B点的坐标.已知了△AOC和△BOC的面积比,由于两三角形的高相等,因此面积比就是AO与OB的比.由此可求出OA的长,也就求出了A点的坐标,然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式.
(1)∵抛物线的对称轴为直线x=1,
∴![]() =1
=1
∴b=-2
∵抛物线与y轴交于点C(0,-3),
∴c=-3,
∴抛物线的函数表达式为y=x2-2x-3;
(2)∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0)
设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,
则![]() ,
,
∴![]()
∴直线BC的函数表达式为y=x-3;
(3)①∵AB=4,PQ=![]() AB,
AB,
∴PQ=3
∵PQ⊥y轴
∴PQ∥x轴,
则由抛物线的对称性可得PM=![]() ,
,
∵对称轴是直线x=1,
∴P到y轴的距离是![]() ,
,
∴点P的横坐标为![]() ,
,
∴P(![]() ,
,![]() )
)
∴F(0,![]() ),
),
∴FC=3-OF=3-![]() =
=![]()
∵PQ垂直平分CE于点F,
∴CE=2FC=![]()
∵点D在直线BC上,
∴当x=1时,y=-2,则D(1,-2),
过点D作DG⊥CE于点G,
∴DG=1,CG=1,
∴GE=CE-CG=![]() -1=
-1=![]() .
.
在Rt△EGD中,tan∠CED=![]() .
.
②P1(1-![]() ,-2),P2(1-
,-2),P2(1-![]() ,-
,-![]() ).
).
设OE=a,则GE=2-a,
当CE为斜边时,则DG2=CGGE,即1=(OC-OG)(2-a),
∴1=1×(2-a),
∴a=1,
∴CE=2,
∴OF=OE+EF=2
∴F、P的纵坐标为-2,
把y=-2,代入抛物线的函数表达式为y=x2-2x-3得:x=1+![]() 或1-
或1-![]()
∵点P在第三象限.
∴P1(1-![]() ,-2),
,-2),
当CD为斜边时,DE⊥CE,
∴OE=2,CE=1,
∴OF=2.5,
∴P和F的纵坐标为:-![]() ,
,
把y=-![]() ,代入抛物线的函数表达式为y=x2-2x-3得:x=1-
,代入抛物线的函数表达式为y=x2-2x-3得:x=1-![]() ,或1+
,或1+![]() ,
,
∵点P在第三象限.
∴P2(1-![]() ,-
,-![]() ).
).
综上所述:满足条件为P1(1-![]() ,-2),P2(1-
,-2),P2(1-![]() ,-
,-![]() ).
).


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
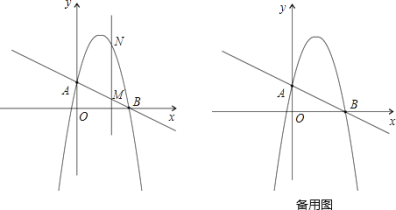
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
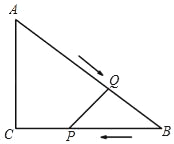
【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为lcm/s;同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动连接PQ,设运动时间为t(s)(0<t<2.5),解答下列问题:
(1)①BQ= ,BP= ;(用含t的代数式表示)
②设△PBQ的面积为y(cm2),试确定y与t的函数关系式;
(2)在运动过程中,是否存在某一时刻t,使△PBQ的面积为△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由;
(3)在运动过程中,是否存在某一时刻t,使△BPQ为等腰三角形?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
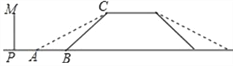
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的![]() 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
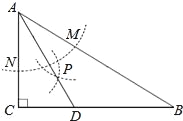
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③△ABD是等腰三角形
④点D到直线AB的距离等于CD的长度.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com