
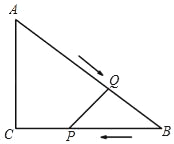
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПCЈҪ90ЎгЈ¬ACЈҪ3cmЈ¬BCЈҪ4cmЈ¬өгPҙУөгBіц·ўЈ¬СШBCПтөгCФИЛЩФЛ¶ҜЈ¬ЛЩ¶ИОӘlcm/sЈ»Н¬КұЈ¬өгQҙУөгAіц·ўЈ¬СШABПтөгBФИЛЩФЛ¶ҜЈ¬ЛЩ¶ИОӘ2cm/sЈ»өұТ»ёцөгНЈЦ№ФЛ¶ҜКұЈ¬БнТ»ёцөгТІНЈЦ№ФЛ¶ҜБ¬ҪУPQЈ¬ЙиФЛ¶ҜКұјдОӘtЈЁsЈ©ЈЁ0ЈјtЈј2.5Ј©Ј¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ўЩBQЈҪЎЎ ЎЎЈ¬BPЈҪЎЎ ЎЎЈ»ЈЁУГә¬tөДҙъКэКҪұнКҫЈ©
ўЪЙиЎчPBQөДГж»эОӘyЈЁcm2Ј©Ј¬КФИ·¶ЁyУлtөДәҜКэ№ШПөКҪЈ»
ЈЁ2Ј©ФЪФЛ¶Ҝ№эіМЦРЈ¬КЗ·сҙжФЪДіТ»КұҝМtЈ¬К№ЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»ЈҝИз№ыҙжФЪЈ¬ЗуіцtөДЦөЈ»І»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©ФЪФЛ¶Ҝ№эіМЦРЈ¬КЗ·сҙжФЪДіТ»КұҝМtЈ¬К№ЎчBPQОӘөИСьИэҪЗРОЈҝИз№ыҙжФЪЈ¬ЗуіцtөДЦөЈ»І»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ўЩ5©Ғ2tЈ¬tўЪy=©Ғ![]() t2+
t2+![]() tЈЁ2Ј©І»ҙжФЪДіТ»КұҝМtЈ¬К№ЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»ЈЁ3Ј©tОӘ
tЈЁ2Ј©І»ҙжФЪДіТ»КұҝМtЈ¬К№ЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»ЈЁ3Ј©tОӘ![]() Гл»т
Гл»т![]() Гл»т
Гл»т![]() ГлКұЈ¬ЎчBPQОӘөИСьИэҪЗРО
ГлКұЈ¬ЎчBPQОӘөИСьИэҪЗРО
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩПИАыУГ№ҙ№Й¶ЁАнЗуіцABЈ¬јҙҝЙөГіцҪбВЫЈ»ўЪ№эөгQЧчQDЎНBCУЪDЈ¬Ҫш¶шөГіцЎчBDQЎЧЎчBCAЈ¬УГtұнКҫіцDQЈ¬ЧоәуУГИэҪЗРОөДГж»э№«КҪјҙҝЙөГіцҪбВЫЈ»
ЈЁ2Ј©ПИЗуіцЎчABCөДГж»эЈ¬ФЩАыУГЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»Ј¬ҪЁБў№ШУЪtөД·ҪіМЈ¬Ҫш¶шЕР¶ПіцҙЛ·ҪіМОЮҪвЈ¬јҙҝЙөГіцҪбВЫЈ»
ЈЁ3Ј©·ЦИэЦЦЗйҝцЈ¬АыУГөИСьИэҪЗРОөДРФЦКәНПаЛЖИэҪЗРОөДРФЦКЈ¬өГіцұИАэКҪҪЁБў№ШУЪtөД·ҪіМЗуҪвЈ¬јҙҝЙөГіцҪбВЫЈ®
ЈЁ1Ј©ўЩФЪRtЎчABCЦРЈ¬ACЈҪ3cmЈ¬BCЈҪ4cmЈ¬
ёщҫЭ№ҙ№Й¶ЁАнөГЈ¬ABЈҪ5cmЈ¬
УЙФЛ¶ҜЦӘЈ¬BPЈҪtЈ¬AQЈҪ2tЈ¬
ЎаBQЈҪAB©ҒAQЈҪ5©Ғ2tЈ¬
№Кҙр°ёОӘЈә5©Ғ2tЈ¬tЈ»
ўЪИзНј1Ј¬№эөгQЧчQDЎНBCУЪDЈ¬

ЎаЎПBDQЈҪЎПCЈҪ90ЎгЈ¬
ЎЯЎПBЈҪЎПBЈ¬
ЎаЎчBDQЎЧЎчBCAЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаDQЈҪ![]() ЈЁ5©Ғ2tЈ©
ЈЁ5©Ғ2tЈ©
ЎаyЈҪSЎчPBQЈҪ![]() BPDQЈҪ
BPDQЈҪ![]() ЎБtЎБ
ЎБtЎБ![]() ЈЁ5©Ғ2tЈ©ЈҪ©Ғ
ЈЁ5©Ғ2tЈ©ЈҪ©Ғ![]() t2+
t2+![]() tЈ»
tЈ»
ЈЁ2Ј©І»ҙжФЪЈ¬
АнУЙЈәЎЯACЈҪ3Ј¬BCЈҪ4Ј¬
ЎаSЎчABCЈҪ![]() ЎБ3ЎБ4ЈҪ6Ј¬
ЎБ3ЎБ4ЈҪ6Ј¬
УЙЈЁ1Ј©ЦӘЈ¬SЎчPBQЈҪ©Ғ![]() t2+
t2+![]() tЈ¬
tЈ¬
ЎЯЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»Ј¬
Ўа©Ғ![]() t2+
t2+![]() tЈҪ3Ј¬
tЈҪ3Ј¬
Ўа2t2©Ғ5t+10ЈҪ0Ј¬
ЎЯЎчЈҪ25©Ғ4ЎБ2ЎБ10Јј0Ј¬
ЎаҙЛ·ҪіМОЮҪвЈ¬
јҙЈәІ»ҙжФЪДіТ»КұҝМtЈ¬К№ЎчPBQөДГж»эОӘЎчABCГж»эөД¶ю·ЦЦ®Т»Ј»
ЈЁ3Ј©УЙЈЁ1Ј©ЦӘЈ¬AQЈҪ2tЈ¬BQЈҪ5©Ғ2tЈ¬BPЈҪtЈ¬
ЎЯЎчBPQКЗөИСьИэҪЗРОЈ¬
ЎаўЩөұBPЈҪBQКұЈ¬
ЎаtЈҪ5©Ғ2tЈ¬
ЎаtЈҪ![]() Ј¬
Ј¬
ўЪөұBPЈҪPQКұЈ¬ИзНј2№эөгPЧчPEЎНABУЪEЈ¬

ЎаBEЈҪ![]() BQЈҪ
BQЈҪ![]() ЈЁ5©Ғ2tЈ©Ј¬
ЈЁ5©Ғ2tЈ©Ј¬
ЎЯЎПBEPЈҪ90ЎгЈҪЎПCЈ¬ЎПBЈҪЎПBЈ¬
ЎаЎчBEPЎЧЎчBCAЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаtЈҪ![]()
ўЫөұBQЈҪPQКұЈ¬ИзНј3Ј¬№эөгQЧчQFЎНBCУЪFЈ¬

ЎаBFЈҪ![]() BPЈҪ
BPЈҪ![]() tЈ¬
tЈ¬
ЎЯЎПBFQЈҪ90ЎгЈҪЎПCЈ¬ЎПBЈҪЎПBЈ¬
ЎаЎчBFQЎЧЎчBCAЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаtЈҪ![]() Ј¬
Ј¬
јҙЈәtОӘ![]() Гл»т
Гл»т![]() Гл»т
Гл»т![]() ГлКұЈ¬ЎчBPQОӘөИСьИэҪЗРОЈ®
ГлКұЈ¬ЎчBPQОӘөИСьИэҪЗРОЈ®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОТГЗ¶ЁТеЈәИзНј1Ј¬ФЪЎчABCҝҙЈ¬°СABөгAЛіКұХлРэЧӘҰБЈЁ0ЎгЈјҰБЈј180ЎгЈ©өГөҪAB'Ј¬°СACИЖөгAДжКұХлРэЧӘҰВөГөҪAC'Ј¬Б¬ҪУB'C'Ј®өұҰБ+ҰВ=180ЎгКұЈ¬ОТГЗіЖЎчA'B'C'КЗЎчABCөДЎ°РэІ№ИэҪЗРОЎұЈ¬ЎчAB'C'ұЯB'C'ЙПөДЦРПЯADҪРЧцЎчABCөДЎ°РэІ№ЦРПЯЎұЈ¬өгAҪРЧцЎ°РэІ№ЦРРДЎұЈ®
МШАэёРЦӘЈә
ЈЁ1Ј©ФЪНј2Ј¬Нј3ЦРЈ¬ЎчAB'C'КЗЎчABCөДЎ°РэІ№ИэҪЗРОЎұЈ¬ADКЗЎчABCөДЎ°РэІ№ЦРПЯЎұЈ®
ўЩИзНј2Ј¬өұЎчABCОӘөИұЯИэҪЗРОКұЈ¬ADУлBCөДКэБҝ№ШПөОӘAD=ЎЎ ЎЎBCЈ»
ўЪИзНј3Ј¬өұЎПBAC=90ЎгЈ¬BC=8КұЈ¬ФтADіӨОӘЎЎ ЎЎЈ®
ІВПлВЫЦӨЈә
ЈЁ2Ј©ФЪНј1ЦРЈ¬өұЎчABCОӘИОТвИэҪЗРОКұЈ¬ІВПлADУлBCөДКэБҝ№ШПөЈ¬ІўёшУиЦӨГчЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
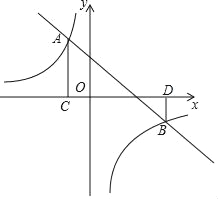
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯy=©Ғx+2Ул·ҙұИАэәҜКэy=![]() ЈЁkЎЩ0Ј©өДНјПуҪ»УЪAЈЁaЈ¬3Ј©Ј¬BЈЁ3Ј¬bЈ©БҪөгЈ¬№эөгAЧчACЎНxЦбУЪөгCЈ¬№эөгBЧчBDЎНxЦбУЪөгDЈ®
ЈЁkЎЩ0Ј©өДНјПуҪ»УЪAЈЁaЈ¬3Ј©Ј¬BЈЁ3Ј¬bЈ©БҪөгЈ¬№эөгAЧчACЎНxЦбУЪөгCЈ¬№эөгBЧчBDЎНxЦбУЪөгDЈ®
(1)ЗуaЈ¬bөДЦөј°·ҙұИАэәҜКэөДҪвОцКҪЈ»
(2)ИфөгPФЪЦұПЯy=©Ғx+2ЙПЈ¬ЗТSЎчACP=SЎчBDPЈ¬ЗлЗуіцҙЛКұөгPөДЧшұкЈ»
(3)ФЪxЦбХэ°лЦбЙПКЗ·сҙжФЪөгMЈ¬К№өГЎчMABОӘөИСьИэҪЗРОЈҝИфҙжФЪЈ¬ЗлЦұҪУРҙіцMөгөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈ¬ФЪН¬Т»ЖҪГжЦұҪЗЧшұкПөЦРЈ¬·ҙұИАэәҜКэyЈҪ![]() Ул¶юҙОәҜКэyЈҪЈӯx2Ј«2xЈ«cөДНјПуҪ»УЪөгA(Јӯ1Ј¬m)Ј®
Ул¶юҙОәҜКэyЈҪЈӯx2Ј«2xЈ«cөДНјПуҪ»УЪөгA(Јӯ1Ј¬m)Ј®
(1)ЗуmЈ¬cөДЦөЈ»
(2)Зу¶юҙОәҜКэНјПуөД¶ФіЖЦбәН¶ҘөгЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
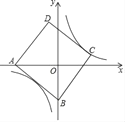
ЎҫМвДҝЎҝИзНјЈ¬Хэ·ҪРОABCDөДұЯіӨОӘ5Ј¬өгAөДЧшұкОӘЈЁ©Ғ4Ј¬0Ј©Ј¬өгBФЪyЦбЙПЈ¬Иф·ҙұИАэәҜКэy=![]() ЈЁkЎЩ0Ј©өДНјПу№эөгCЈ¬ФтёГ·ҙұИАэәҜКэөДұнҙпКҪОӘ_______Ј®
ЈЁkЎЩ0Ј©өДНјПу№эөгCЈ¬ФтёГ·ҙұИАэәҜКэөДұнҙпКҪОӘ_______Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
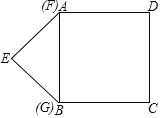
ЎҫМвДҝЎҝИзНјЈ¬ұЯіӨОӘ4ёцөҘО»іӨ¶ИөДХэ·ҪРОABCDөДұЯABУлөИСьЦұҪЗИэҪЗРОEFGөДРұұЯFGЦШәПЈ¬ЎчEFGТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИСШBCПтУТФИЛЩФЛ¶ҜЈЁұЈіЦFGЎНBCЈ©Ј¬өұөгEФЛ¶ҜөҪCDұЯЙПКұЎчEFGНЈЦ№ФЛ¶ҜЈ¬ЙиЎчEFGөДФЛ¶ҜКұјдОӘtГлЈ¬ЎчEFGУлХэ·ҪРОABCDЦШөюІҝ·ЦөДГж»эОӘSЈ¬ФтS№ШУЪtөДәҜКэҙуЦВНјПуОӘЈЁЎЎЈ©
A. 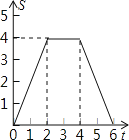 B.
B. 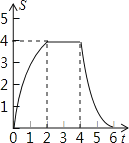 C.
C. 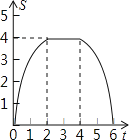 D.
D. 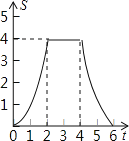
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
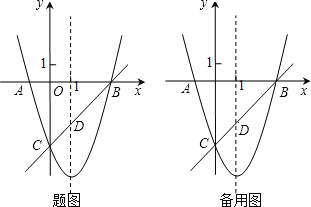
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЕЧОпПЯy=x2Ј«bxЈ«cУлxЦбҪ»УЪAЎўBБҪөгЈЁAөгФЪBөгЧуІаЈ©Ј¬УлyЦбҪ»УЪөгCЈЁ0Ј¬Јӯ3Ј©Ј¬¶ФіЖЦбКЗЦұПЯx=1Ј¬ЦұПЯBCУлЕЧОпПЯөД¶ФіЖЦбҪ»УЪөгDЈ®
ЈЁ1Ј©ЗуЕЧОпПЯөДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©ЗуЦұПЯBCөДәҜКэұнҙпКҪЈ»
ЈЁ3Ј©өгEОӘyЦбЙПТ»¶ҜөгЈ¬CEөДҙ№ЦұЖҪ·ЦПЯҪ»CEУЪөгFЈ¬Ҫ»ЕЧОпПЯУЪPЎўQБҪөгЈ¬ЗТөгPФЪөЪИэПуПЮЈ®
ўЩөұПЯ¶ОPQ=![]() ABКұЈ¬ЗуtanЎПCEDөДЦөЈ»
ABКұЈ¬ЗуtanЎПCEDөДЦөЈ»
ўЪөұТФөгCЎўDЎўEОӘ¶ҘөгөДИэҪЗРОКЗЦұҪЗИэҪЗРОКұЈ¬ЗлЦұҪУРҙіцөгPөДЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ABОӘЎСOөДЦұҫ¶Ј¬CОӘЎСOЙПТ»өгЈ¬ЎПABCөДЖҪ·ЦПЯҪ»ЎСOУЪөгDЈ¬DEЎНBCУЪөгEЈ®
ЈЁ1Ј©КФЕР¶ПDEУлЎСOөДО»ЦГ№ШПөЈ¬ІўЛөГчАнУЙЈ»
ЈЁ2Ј©№эөгDЧчDFЎНABУЪөгFЈ¬ИфBE=3![]() Ј¬DF=3Ј¬ЗуНјЦРТхУ°Іҝ·ЦөДГж»эЈ®
Ј¬DF=3Ј¬ЗуНјЦРТхУ°Іҝ·ЦөДГж»эЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪХэ·ҪРОЦҪЖ¬ABCDЦРЈ¬¶ФҪЗПЯACЎўBDҪ»УЪөгOЈ¬ХЫөюХэ·ҪРОЦҪЖ¬ ABCDЈ¬К№ADВдФЪBDЙПЈ¬өгAЗЎәГУлBDЙПөДөгFЦШәП.Х№ҝӘәуЈ¬ХЫәЫDE·ЦұрҪ»ABЎў ACУЪөгEЎўG.Б¬ҪУGF.ФтПВБРҪбВЫҙнОуөДКЗ( )
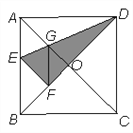
A. ЎПAGD=112.5Ўг B. ЛДұЯРОAEFGКЗБвРО C. tanЎПAED=2 D. BE=2OG
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com