
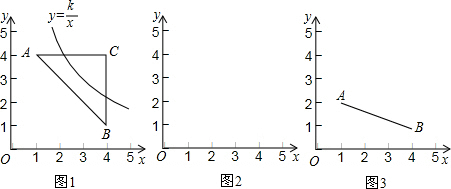
Ζ÷Έω Θ®1Θ©Ζ÷±π«σΒΟΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κ±ΏACΘ§±ΏBC”–ΙΪΙ≤ΒψΒΡkΒΡ»Γ÷ΒΖΕΈßΘ§»ΜΚσ«σΒΟ÷±œΏABΒΡΫβΈω ΫΘ§άϊ”Ο“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΗυΒΡ≈–±π Ϋ«σΒΟ”κ±ΏAB”–ΙΪΙ≤ΒψΒΡkΒΡ»Γ÷ΒΖΕΈßΘ§‘ρΩ…«σΒΟ¥πΑΗΘΜ
Θ®2Θ© Ήœ»«σΒΟΒψCΒΡΉχ±ξΘ§Φ¥Ω…ΒΟΥΪ«ζœΏy=$\frac{m}{x}$Θ®xΘΨ0Θ©”κ±ΏACΘ§±ΏBC”–ΙΪΙ≤ΒψΒΡkΒΡ»Γ÷ΒΖΕΈßΘ§”…Θ®1Θ©Ω…«σΒΟ”κ±ΏABΒΡ»Γ÷ΒΖΕΈßΘ§ΦΧΕχ«σΒΟ¥πΑΗΘΜ
Θ®3Θ© Ήœ»«σΒΟœΏΕΈABΒΡΫβΈω Ϋ“‘ΦΑΉ‘±δΝΩΒΡ»Γ÷ΒΖΕΈßΘ§‘Όάϊ”Ο“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΗυΒΡ≈–±π Ϋ«σΒΟ¥πΑΗΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…η÷±œΏABΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
ΓΏAΘ®1Θ§4Θ©ΓΔBΘ®4Θ§1Θ©Θ§
Γύ$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$Θ§
ΫβΒΟΘΚ$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$Θ§
Γύ÷±œΏABΒΡΫβΈω ΫΈΣΘΚy=-x+5Θ§
ΓΏΓςABC»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®1Θ§4Θ©ΓΔBΘ®4Θ§1Θ©ΓΔCΘ®4Θ§4Θ©Θ§
Γύ»τΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κ±ΏAC”–ΙΪΙ≤ΒψΘ§‘ρ4ΓήkΓή16Θ§
»τΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κ±ΏBC”–ΙΪΙ≤ΒψΘ§‘ρ4ΓήkΓή16Θ§
»τΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κ±ΏAB”–ΙΪΙ≤ΒψΘ§‘ρ$\frac{k}{x}$=-x+5Θ®1ΓήxΓή4Θ©Θ§
Φ¥x2-5x+k=0Θ§
ΓύΓς=25-4kΓί0Θ§
ΫβΒΟΘΚkΓή$\frac{25}{4}$Θ§
Γύ»τΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κ±ΏAB”–ΙΪΙ≤ΒψΘ§‘ρ4ΓήkΓή$\frac{25}{4}$ΘΜ
Ήέ…œΩ…ΒΟΘΚ»τΥΪ«ζœΏy=$\frac{k}{x}$Θ®xΘΨ0Θ©”κΓςABC”–ΙΪΙ≤ΒψΘ§‘ρkΒΡ»Γ÷ΒΖΕΈß «ΘΚ4ΓήkΓή16ΘΜ
Ι ¥πΑΗΈΣΘΚ4ΓήkΓή16ΘΜ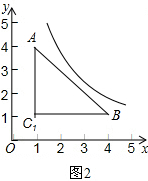 Θ®2Θ©»γΆΦΘ§‘ρΒψC1Θ®1Θ§1Θ©Θ§
Θ®2Θ©»γΆΦΘ§‘ρΒψC1Θ®1Θ§1Θ©Θ§
”…Θ®1Θ©ΒΟΘΚ»τΥΪ«ζœΏy=$\frac{m}{x}$Θ®xΘΨ0Θ©”κ±ΏAB”–ΙΪΙ≤ΒψΘ§‘ρ4ΓήmΓή$\frac{25}{4}$Θ§
ΓΏ»τΥΪ«ζœΏy=$\frac{m}{x}$Θ®xΘΨ0Θ©”κ±ΏAC”–ΙΪΙ≤ΒψΘ§‘ρ1ΓήkΓή4Θ§
»τΥΪ«ζœΏy=$\frac{m}{x}$Θ®xΘΨ0Θ©”κ±ΏBC”–ΙΪΙ≤ΒψΘ§‘ρ1ΓήkΓή4Θ§
Ήέ…œΩ…ΒΟΘΚ»τΥΪ«ζœΏy=$\frac{m}{x}$Θ®xΘΨ0Θ©”κΓςABC”–ΙΪΙ≤ΒψΘ§‘ρkΒΡ»Γ÷ΒΖΕΈß «ΘΚ1ΓήkΓή$\frac{25}{4}$ΘΜ
Θ®3Θ©»γΆΦ3Θ§…η÷±œΏABΒΡΫβΈω ΫΈΣΘΚy=mx+nΘ§
ΓΏΒψAΈΣΘ®1Θ§2Θ©Θ§ΒψBΈΣΘ®4Θ§1Θ©Θ§
Γύ$\left\{\begin{array}{l}{m+n=2}\\{4m+n=1}\end{array}\right.$Θ§
ΫβΒΟΘΚ$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=\frac{7}{3}}\end{array}\right.$Θ§
Γύ÷±œΏABΒΡΫβΈω ΫΈΣΘΚy=-$\frac{1}{3}$x+$\frac{7}{3}$Θ®1ΓήxΓή4Θ©Θ§
»τΥΪ«ζœΏy=$\frac{n}{x}$Θ®xΘΨ0Θ©”κœΏΕΈAB”–ΙΪΙ≤ΒψΘ§
‘ρ$\frac{n}{x}$=-$\frac{1}{3}$x+$\frac{7}{3}$Θ§
’ϊάμΒΟΘΚx2-7x+3n=0Θ§
ΓύΓς=49-12nΓί0Θ§
ΓύnΓή$\frac{49}{12}$Θ§
ΓΏ1ΓήxΓή4Θ§
ΓύnΓί2Θ§
Γύ»τΥΪ«ζœΏy=$\frac{n}{x}$Θ®xΘΨ0Θ©”κœΏΕΈAB”–ΙΪΙ≤ΒψΘ§‘ρnΒΡ»Γ÷ΒΖΕΈß «ΘΚ2ΓήnΓή$\frac{49}{12}$Θ°
Ι ¥πΑΗΈΣΘΚ2ΓήnΓή$\frac{49}{12}$Θ°
ΒψΤά ¥ΥΧβ τ”ΎΖ¥±»άΐΚ· ΐΉέΚœΧβΘ§ΩΦ≤ιΝΥ÷±œΏ”κΖ¥±»άΐΚ· ΐΒΡΫΜΒψΈ Χβ“‘ΦΑ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυΒΡ≈–±π ΫΘ°ΉΔ“βΡήΫη÷ζ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΗυΒΡ≈–Εœ Ϋ«σΫβ «ΙΊΦϋΘ°


 άΦΆΑΌΆ®÷ςΧεΩΈΧΟ–Γ―ßΩΈ ±Ά§≤Ϋ¥ο±ξœΒΝ–¥πΑΗ
άΦΆΑΌΆ®÷ςΧεΩΈΧΟ–Γ―ßΩΈ ±Ά§≤Ϋ¥ο±ξœΒΝ–¥πΑΗ άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ
άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ ΑΌΖ÷―ß…ζΉς“Β±ΨΧβΝΖΆθœΒΝ–¥πΑΗ
ΑΌΖ÷―ß…ζΉς“Β±ΨΧβΝΖΆθœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -3 | BΘ° | 3 | CΘ° | -$\frac{1}{3}$ | DΘ° | $\frac{1}{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{4}$=Γά2 | BΘ° | 3-1=-$\frac{1}{3}$ | CΘ° | Θ®-1Θ©2015=-1 | DΘ° | |-2|=-2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 30 | BΘ° | 26 | CΘ° | 10 | DΘ° | 6 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2Θ§2 | BΘ° | 2Θ§3 | CΘ° | 3Θ§4 | DΘ° | 4Θ§4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
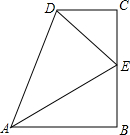 »γΆΦΥυ ΨΘ§ABΓΈCDΘ§ΓœB=90ΓψΘ§E «BCΒΡ÷–ΒψΘ§DEΤΫΖ÷ΓœADCΘ§«σ÷ΛΘΚAEΤΫΖ÷ΓœDABΘ°
»γΆΦΥυ ΨΘ§ABΓΈCDΘ§ΓœB=90ΓψΘ§E «BCΒΡ÷–ΒψΘ§DEΤΫΖ÷ΓœADCΘ§«σ÷ΛΘΚAEΤΫΖ÷ΓœDABΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1Ηω | BΘ° | 2Ηω | CΘ° | 3Ηω | DΘ° | 4Ηω |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
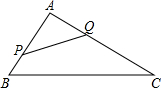 »γΆΦΘ§‘Ύ»ΐΫ«–ΈABC÷–Θ§AB=8Θ§AC=16Θ§ΒψP¥”ΒψBΩΣ Φ―Ί±ΏBAœρΒψA“‘2άεΟΉΟΩΟκΒΡΥΌΕ»“ΤΕ·Θ§ΒψQ¥”ΒψAœρΒψC“‘4άεΟΉΟΩΟκΒΡΥΌΕ»“ΤΕ·Θ§»γΙϊΒψPΓΔQΖ÷±π¥”ΒψBΓΔAΆ§ ±≥ωΖΔΘ§Ψ≠ΙΐΕύ…ΌΟκ ±Θ§“‘AΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ»ΐΫ«–ΈABCœύΥΤΘΩ
»γΆΦΘ§‘Ύ»ΐΫ«–ΈABC÷–Θ§AB=8Θ§AC=16Θ§ΒψP¥”ΒψBΩΣ Φ―Ί±ΏBAœρΒψA“‘2άεΟΉΟΩΟκΒΡΥΌΕ»“ΤΕ·Θ§ΒψQ¥”ΒψAœρΒψC“‘4άεΟΉΟΩΟκΒΡΥΌΕ»“ΤΕ·Θ§»γΙϊΒψPΓΔQΖ÷±π¥”ΒψBΓΔAΆ§ ±≥ωΖΔΘ§Ψ≠ΙΐΕύ…ΌΟκ ±Θ§“‘AΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ»ΐΫ«–ΈABCœύΥΤΘΩ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com