
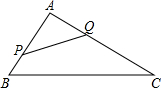
 如图,在三角形ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2厘米每秒的速度移动,点Q从点A向点C以4厘米每秒的速度移动,如果点P、Q分别从点B、A同时出发,经过多少秒时,以A、P、Q为顶点的三角形与三角形ABC相似?
如图,在三角形ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2厘米每秒的速度移动,点Q从点A向点C以4厘米每秒的速度移动,如果点P、Q分别从点B、A同时出发,经过多少秒时,以A、P、Q为顶点的三角形与三角形ABC相似? 分析 设经过t秒时,以A、P、Q为顶点的三角形与三角形ABC相似,则BP=2t,AP=8-2t,AQ=4t,利用两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论:当$\frac{AP}{AB}$=$\frac{AQ}{AC}$时,△APQ∽△ABC,即$\frac{8-2t}{8}$=$\frac{4t}{16}$;当$\frac{AP}{AC}$=$\frac{AQ}{AB}$时,△APQ∽△ACB,即$\frac{8-2t}{16}$=$\frac{4t}{8}$,然后分别解方程即可.
解答 解:设经过t秒时,以A、P、Q为顶点的三角形与三角形ABC相似,则BP=2t,AP=8-2t,AQ=4t,
∵∠PAQ=∠BAC,
∴当$\frac{AP}{AB}$=$\frac{AQ}{AC}$时,△APQ∽△ABC,即$\frac{8-2t}{8}$=$\frac{4t}{16}$,解得t=2(s);
当$\frac{AP}{AC}$=$\frac{AQ}{AB}$时,△APQ∽△ACB,即$\frac{8-2t}{16}$=$\frac{4t}{8}$,解得t=0.8(s);
即经过2秒或0.8秒时,以A、P、Q为顶点的三角形与三角形ABC相似.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.会利用时间表示相应线段的长,注意分类讨论思想的运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
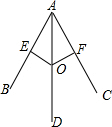 如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{3}$AB,AF=$\frac{1}{3}$AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.
如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{3}$AB,AF=$\frac{1}{3}$AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
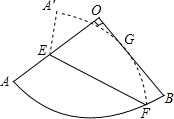 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A′F}$恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com